Real Exponents
... (since 2x is an increasing function for rational x). Also, since 2 < 2, the sequence of approximations are all less than 22 = 4. A basic ...
... (since 2x is an increasing function for rational x). Also, since 2 < 2, the sequence of approximations are all less than 22 = 4. A basic ...
國立嘉義大學102學年度基礎學科學力競賽試題卷: 科目: 經濟數學 題
... 9. An appliance store manager estimates that for x television ads run per day, R( x) 0.01x3 x 2 3x 200 refrigerators will be sold per month. Find R (4) and interpret what it tells us about sales. A) R (4) 4.52; sales will be increasing at about 5 refrigerators per month per ...
... 9. An appliance store manager estimates that for x television ads run per day, R( x) 0.01x3 x 2 3x 200 refrigerators will be sold per month. Find R (4) and interpret what it tells us about sales. A) R (4) 4.52; sales will be increasing at about 5 refrigerators per month per ...
Name: Period: Chapter 1 Review Use the review examples and
... Step 4: Look Back: Use estimation. Since L 10 and A=60, w 6 . Then P 210 26 32 feet, so your answer is reasonable. Exercises: ...
... Step 4: Look Back: Use estimation. Since L 10 and A=60, w 6 . Then P 210 26 32 feet, so your answer is reasonable. Exercises: ...
MATH 2241 – Calculus for Business, Social and Life Sciences
... A scientific calculator is required; a graphing calculator is strongly recommended. ...
... A scientific calculator is required; a graphing calculator is strongly recommended. ...
1332Functions1.pdf
... In this example, set K is the domain, and set C is the co-domain. The previous example helps convey the idea of a function, but we will mostly be interested in functions that are sets of ordered pairs of real numbers. If we restrict our discussion to relations and functions that are sets of ordered ...
... In this example, set K is the domain, and set C is the co-domain. The previous example helps convey the idea of a function, but we will mostly be interested in functions that are sets of ordered pairs of real numbers. If we restrict our discussion to relations and functions that are sets of ordered ...
Slide 1
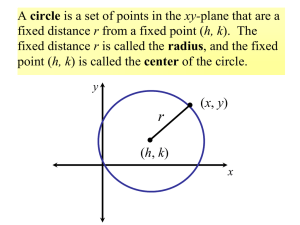
... A circle is a set of points in the xy-plane that are a fixed distance r from a fixed point (h, k). The fixed distance r is called the radius, and the fixed point (h, k) is called the center of the circle. y ...
... A circle is a set of points in the xy-plane that are a fixed distance r from a fixed point (h, k). The fixed distance r is called the radius, and the fixed point (h, k) is called the center of the circle. y ...
Full text
... and q(ri) := the number of partitions of n into distinct parts. We define ^(0) : = 1 and q(ri) := 0 for n< 0. The function #(«), ^ e N, is generated by the infinite product expansion ...
... and q(ri) := the number of partitions of n into distinct parts. We define ^(0) : = 1 and q(ri) := 0 for n< 0. The function #(«), ^ e N, is generated by the infinite product expansion ...
Full text
... In the present note we shall give two proofs of a property of the poly-Bernoulli numbers, the closed formula for negative index poly-Bernoulli numbers given by Arakawa and Kaneko [1]. The first proof uses weighted Stirling numbers of the second kind (see [2], [3]). The second, much simpler, proof is ...
... In the present note we shall give two proofs of a property of the poly-Bernoulli numbers, the closed formula for negative index poly-Bernoulli numbers given by Arakawa and Kaneko [1]. The first proof uses weighted Stirling numbers of the second kind (see [2], [3]). The second, much simpler, proof is ...