Tech Math 2 Lecture Notes, Section 13.2
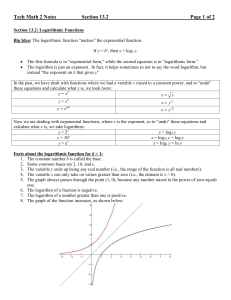
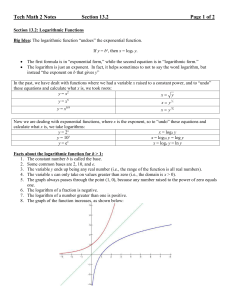
... Now we are dealing with exponential functions, where x is the exponent, so to “undo” these equations and calculate what x is, we take logarithms: y = 2x x = log2 y y = 10x x = log10 y = log y y = ex x = loge y = ln y Facts about the logarithmic function for b > 1: 1. The constant number b is called ...
... Now we are dealing with exponential functions, where x is the exponent, so to “undo” these equations and calculate what x is, we take logarithms: y = 2x x = log2 y y = 10x x = log10 y = log y y = ex x = loge y = ln y Facts about the logarithmic function for b > 1: 1. The constant number b is called ...
Practicals 1 - Roxana Dumitrescu
... 2π For x ≤ 0 you can use the same formula to evaluate 1 − N (−x). The formula can be derived by choosing the general functional form and then finding the coefficients that give the best fit. For this question, you should just accept the formula on face value. Write a function called normcdf to evalu ...
... 2π For x ≤ 0 you can use the same formula to evaluate 1 − N (−x). The formula can be derived by choosing the general functional form and then finding the coefficients that give the best fit. For this question, you should just accept the formula on face value. Write a function called normcdf to evalu ...
Functions—3.1 & 3.2
... a) Take out x’s that make a denominator zero. Set denominator = 0 to find numbers to omit from the domain. b) Take out x’s that cause imaginary numbers (even roots of negative radicands). (Set radicand ≥ 0 to find x’s that work. c) Take out x’s for which the argument of a logarithm is negative. (Thi ...
... a) Take out x’s that make a denominator zero. Set denominator = 0 to find numbers to omit from the domain. b) Take out x’s that cause imaginary numbers (even roots of negative radicands). (Set radicand ≥ 0 to find x’s that work. c) Take out x’s for which the argument of a logarithm is negative. (Thi ...
+1,0
... Imaginary numbers do not touch the x-axis. They are not zero’s. (+2,0) are the only zero’s ...
... Imaginary numbers do not touch the x-axis. They are not zero’s. (+2,0) are the only zero’s ...
19 through 29
... Proof. Here we have three functions and three definitions of limits, one for each function. Therefore we have to deal with three δ-s. We shall give them appropriate names that will distinguish them from each other. Let us name them δf , δg and δh . In the theorem it is assumed that lim f (x) = L. Th ...
... Proof. Here we have three functions and three definitions of limits, one for each function. Therefore we have to deal with three δ-s. We shall give them appropriate names that will distinguish them from each other. Let us name them δf , δg and δh . In the theorem it is assumed that lim f (x) = L. Th ...
Notes on Calculus by
... One says that c is a minimum and d a maximum of f on [a, b]. While this is a very beautiful result, we do not see how one can go about finding the points c and d where the extremal values occur. Things become nicer when f is differentiable on (a, b), and even nicer when f is twice differentiable on (a, ...
... One says that c is a minimum and d a maximum of f on [a, b]. While this is a very beautiful result, we do not see how one can go about finding the points c and d where the extremal values occur. Things become nicer when f is differentiable on (a, b), and even nicer when f is twice differentiable on (a, ...
Lecture 11: the Euler φ-function In the light of the previous lecture
... Lecture 11: the Euler φ-function In the light of the previous lecture, we shall now look in more detail at the function defined there. Let n ≥ 1 be a natural number. Recall that we defined φ(n) to be the number of natural numbers 1 ≤ m ≤ n and coprime to n. This function is called Euler’s φ-function ...
... Lecture 11: the Euler φ-function In the light of the previous lecture, we shall now look in more detail at the function defined there. Let n ≥ 1 be a natural number. Recall that we defined φ(n) to be the number of natural numbers 1 ≤ m ≤ n and coprime to n. This function is called Euler’s φ-function ...
Solutions - Math.utah.edu
... • Between two rational numbers there is an irrational number. • Between two irrational numbers there is an rational number. Proof. The proof of the second part was already done in Extra Problems #3, Exercise 0.4 (in fact, we showed there were infinitely many rational numbers between any two numbers) ...
... • Between two rational numbers there is an irrational number. • Between two irrational numbers there is an rational number. Proof. The proof of the second part was already done in Extra Problems #3, Exercise 0.4 (in fact, we showed there were infinitely many rational numbers between any two numbers) ...
Document
... Definition: The cardinality of an infinite set S that is countable is denotes by א0 (where אis aleph, the first letter of the Hebrew alphabet). We write |S| = א0 and say that S has cardinality “aleph null”. Note: Georg Cantor defined the notion of cardinality and was the first to realize that ...
... Definition: The cardinality of an infinite set S that is countable is denotes by א0 (where אis aleph, the first letter of the Hebrew alphabet). We write |S| = א0 and say that S has cardinality “aleph null”. Note: Georg Cantor defined the notion of cardinality and was the first to realize that ...
Full text
... so that in this case ak+l might be in the interval (0, k + 3] ... . The proof of the theorem leads to the construction of a sequence s(N, a) with a-a and N = 0 as defined in the introduction. Now, suppose a G[0, 2] is a rational number of the form k 12m with k, m eN0. Then at is a rational number wi ...
... so that in this case ak+l might be in the interval (0, k + 3] ... . The proof of the theorem leads to the construction of a sequence s(N, a) with a-a and N = 0 as defined in the introduction. Now, suppose a G[0, 2] is a rational number of the form k 12m with k, m eN0. Then at is a rational number wi ...
Algebra I STAAR Review Twilight Bingo
... The amount an appliance repairman charges for each job is represented by the function t = 50h + 35, where h represents the number of hours he spent on the job and t represents the total amount he charges in dollars for the job. The repairman plans to change the amount he charges for each job. Th ...
... The amount an appliance repairman charges for each job is represented by the function t = 50h + 35, where h represents the number of hours he spent on the job and t represents the total amount he charges in dollars for the job. The repairman plans to change the amount he charges for each job. Th ...