TEACHER MODELING/STUDENT
... the multiplication equation represents four times the number of shaded parts in a 5/6 bar. This provides a connection between multiplication involving whole numbers and fractions. 3. Find any whole Fraction Bar and write the multiplication equation for 5 times the fraction for the bar. (Look at some ...
... the multiplication equation represents four times the number of shaded parts in a 5/6 bar. This provides a connection between multiplication involving whole numbers and fractions. 3. Find any whole Fraction Bar and write the multiplication equation for 5 times the fraction for the bar. (Look at some ...
Grade 7 Math Expressions and Equations
... Standard 7.EE.3 Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appro ...
... Standard 7.EE.3 Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations to calculate with numbers in any form; convert between forms as appro ...
On the least prime in certain arithmetic
... The usual method used to nd large gaps between successive prime numbers is to construct a long sequence S of consecutive integers, each of which has a \small" prime factor (so that they cannot be prime); then, the gap between the largest prime before S and the next, is at least as long as S . Simil ...
... The usual method used to nd large gaps between successive prime numbers is to construct a long sequence S of consecutive integers, each of which has a \small" prime factor (so that they cannot be prime); then, the gap between the largest prime before S and the next, is at least as long as S . Simil ...
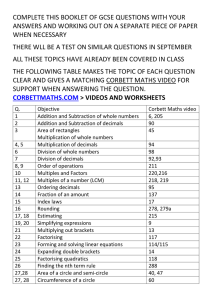
corbett maths video - Acland Burghley School
... Addition and Subtraction of whole numbers Addition and Subtraction of decimals Area of rectangles Multiplication of whole numbers Multiplication of decimals Division of whole numbers Division of decimals Order of operations Multiples and Factors Multiples of a number (LCM) ...
... Addition and Subtraction of whole numbers Addition and Subtraction of decimals Area of rectangles Multiplication of whole numbers Multiplication of decimals Division of whole numbers Division of decimals Order of operations Multiples and Factors Multiples of a number (LCM) ...
Arithmetic & Logic Part 2
... In two’s complement, the same algorithm is applied to the operands regardless of the sign. Adding two numbers is done by simply applying the same algorithm used for unsigned numbers. Subtraction can be performed simply by adding the additive inverse of the subtrahend. ...
... In two’s complement, the same algorithm is applied to the operands regardless of the sign. Adding two numbers is done by simply applying the same algorithm used for unsigned numbers. Subtraction can be performed simply by adding the additive inverse of the subtrahend. ...
adding-subtracting-real-numbers-1-2
... First substitute –14 for x. To subtract –12, add 12. When the signs of the numbers are different, find the difference of the absolute values: 14 – 12 = 2. ...
... First substitute –14 for x. To subtract –12, add 12. When the signs of the numbers are different, find the difference of the absolute values: 14 – 12 = 2. ...
Section 4 - North Allegheny School District
... multiple of two or more numbers Least common denominator (LCD) – the least common multiple of the denominators of two or more fractions ...
... multiple of two or more numbers Least common denominator (LCD) – the least common multiple of the denominators of two or more fractions ...
Floating-point Arithmetic
... small perturbations in the input could lead to large perturbations in the output. – The algorithm may be poorly designed: ...
... small perturbations in the input could lead to large perturbations in the output. – The algorithm may be poorly designed: ...
1-2 - Plain Local Schools
... First substitute –14 for x. To subtract –12, add 12. When the signs of the numbers are different, find the difference of the absolute values: 14 – 12 = 2. ...
... First substitute –14 for x. To subtract –12, add 12. When the signs of the numbers are different, find the difference of the absolute values: 14 – 12 = 2. ...
Measurements, Sig Figs and Graphing
... Characteristic = number on left of decimal= power of 10 Mantissa = number on right of decimal g # of sig figs ...
... Characteristic = number on left of decimal= power of 10 Mantissa = number on right of decimal g # of sig figs ...
SS2.1 Simplifying Algebraic Expressions
... dollars more than five times as much for the bike as the helmet. What was the price of the bike? (Note: The phrase “as much as” can be tricky because sometimes it is split up. The as much as is what is being multiplied and the phrasing “for such and such” is what the product is equivalent to. ie 5he ...
... dollars more than five times as much for the bike as the helmet. What was the price of the bike? (Note: The phrase “as much as” can be tricky because sometimes it is split up. The as much as is what is being multiplied and the phrasing “for such and such” is what the product is equivalent to. ie 5he ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.