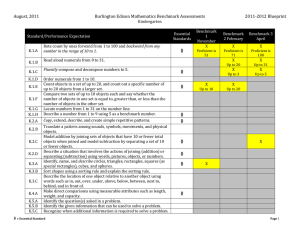
Lab 8 (10 points) Please sign in the sheet and submit the
... In mathematics, the Fibonacci numbers are a sequence of numbers named after Leonardo of Pisa, known as Fibonacci. The first number of the sequence is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself, yielding the sequence 0, ...
... In mathematics, the Fibonacci numbers are a sequence of numbers named after Leonardo of Pisa, known as Fibonacci. The first number of the sequence is 0, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself, yielding the sequence 0, ...
Interesting problems from the AMATYC Student Math League Exams
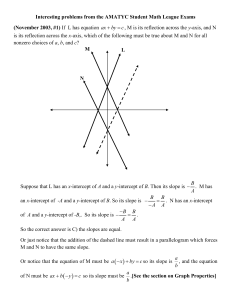
... (November 2003, #17) A boat with an ill passenger is 7½ miles north of a straight coastline which runs east and west. A hospital on the coast is 60 miles from the point on shore south of the boat. If the boat starts toward shore at 15 mph at the same time an ambulance leaves the hospital at 60 mph a ...
... (November 2003, #17) A boat with an ill passenger is 7½ miles north of a straight coastline which runs east and west. A hospital on the coast is 60 miles from the point on shore south of the boat. If the boat starts toward shore at 15 mph at the same time an ambulance leaves the hospital at 60 mph a ...
Number systems - The Open University
... 2 Complex numbers 2.1 What is a complex number? We will now discuss complex numbers and their properties. We will show how they can be represented as points in the plane and state the Fundamental Theorem of Algebra: that any polynomial equation with complex coefficients has a solution which is a com ...
... 2 Complex numbers 2.1 What is a complex number? We will now discuss complex numbers and their properties. We will show how they can be represented as points in the plane and state the Fundamental Theorem of Algebra: that any polynomial equation with complex coefficients has a solution which is a com ...
Discrete Math CS 2800
... How can we assign a memory location to a record so that later on it’s easy to locate and retrieve such a record? Solution to this problem a good hashing function. Records are identified using a key (k), which uniquely identifies each record. If you compute the hash of the same data at different ti ...
... How can we assign a memory location to a record so that later on it’s easy to locate and retrieve such a record? Solution to this problem a good hashing function. Records are identified using a key (k), which uniquely identifies each record. If you compute the hash of the same data at different ti ...
The Division Theorem • Theorem Let n be a fixed integer ≥ 2. For
... • Simple pseudo-random number generators can be given using modular arithmetic. We choose a large modulus, often related to word size in memory, like 231 −1. Then we choose an integer seed a0, using it as the base case for an inductive definition an+1 = (16, 807 · an) mod (231 − 1). (The number 16,8 ...
... • Simple pseudo-random number generators can be given using modular arithmetic. We choose a large modulus, often related to word size in memory, like 231 −1. Then we choose an integer seed a0, using it as the base case for an inductive definition an+1 = (16, 807 · an) mod (231 − 1). (The number 16,8 ...
Interesting problems from the AMATYC Student Math League Exams
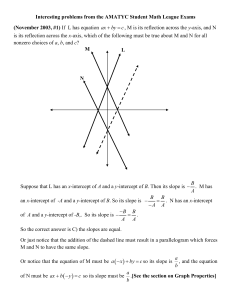
... (November 2003, #17) A boat with an ill passenger is 7½ miles north of a straight coastline which runs east and west. A hospital on the coast is 60 miles from the point on shore south of the boat. If the boat starts toward shore at 15 mph at the same time an ambulance leaves the hospital at 60 mph a ...
... (November 2003, #17) A boat with an ill passenger is 7½ miles north of a straight coastline which runs east and west. A hospital on the coast is 60 miles from the point on shore south of the boat. If the boat starts toward shore at 15 mph at the same time an ambulance leaves the hospital at 60 mph a ...
AN INVITATION TO ADDITIVE PRIME NUMBER THEORY A. V.
... With the exception of the bound G(3) ≤ 7, all of these results have been obtained by an iterative version of the circle method that originated in the work of Davenport [46, 48] and Davenport and Erdös [50]. The bound for G(3) was established first by Linnik [141] and until recently lay beyond the r ...
... With the exception of the bound G(3) ≤ 7, all of these results have been obtained by an iterative version of the circle method that originated in the work of Davenport [46, 48] and Davenport and Erdös [50]. The bound for G(3) was established first by Linnik [141] and until recently lay beyond the r ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.