Trigonometric Functions and Complex Numbers
... In the previous section, the ratio, y / x , is adopted to map to the angle θ. There are five more such possibilities: x / y , x / r , r / x , y / r and r / y . We thus define a total of six functions as listed in Table 1. The basic relationships among themselves are given in square brackets. Three f ...
... In the previous section, the ratio, y / x , is adopted to map to the angle θ. There are five more such possibilities: x / y , x / r , r / x , y / r and r / y . We thus define a total of six functions as listed in Table 1. The basic relationships among themselves are given in square brackets. Three f ...
1 errors - New Age International
... The magnitude of the error in the value of the function due to cutting (truncation) of its series is equal to the sum of all the discarded terms. It may be large and may even exceed the sum of the terms retained, thus making the calculated result meaningless. (iii) Round-off Errors: When depicting e ...
... The magnitude of the error in the value of the function due to cutting (truncation) of its series is equal to the sum of all the discarded terms. It may be large and may even exceed the sum of the terms retained, thus making the calculated result meaningless. (iii) Round-off Errors: When depicting e ...
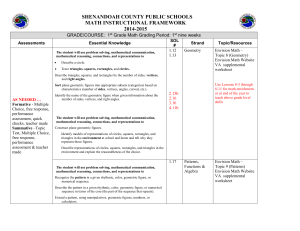
Assessments - Shenandoah County Public Schools
... Model an equation that represents the relationship of two expressions of equal value. ...
... Model an equation that represents the relationship of two expressions of equal value. ...
... a. Ask your family for some important events and the years they occurred in your family’s history, such as the year someone was born or married. Go back as far as you can, for instance the year one of your grandparents was born. Find at least 10 events and their dates. b. Make a list of important ...
Math Continuum as DOC - Texas School for the Blind and
... 1. Associates groups of hundreds with appropriate numeral 2. Writes thousands, hundreds, tens, and ones in compact form 3. Expand a 4-digit numeral into thousands, hundreds, tens, ones. 4. Writes 4-digit numeral associated with number word CLUSTER 41 1. Associates groups of thousands with appropriat ...
... 1. Associates groups of hundreds with appropriate numeral 2. Writes thousands, hundreds, tens, and ones in compact form 3. Expand a 4-digit numeral into thousands, hundreds, tens, ones. 4. Writes 4-digit numeral associated with number word CLUSTER 41 1. Associates groups of thousands with appropriat ...
Mental arithmetic skills book
... numbers that, when they are added together, make a significant number (like 10, 20, 50, 100, 200, 500, 1,000). It is really important to: know some number bond facts be able to quickly use strategies to work out other number bond facts The following number bonds need to be learnt: Set 1: Bonds o ...
... numbers that, when they are added together, make a significant number (like 10, 20, 50, 100, 200, 500, 1,000). It is really important to: know some number bond facts be able to quickly use strategies to work out other number bond facts The following number bonds need to be learnt: Set 1: Bonds o ...
Number systems and sets - Cambridge University Press
... This chapter introduces set notation and discusses sets of numbers and their properties. Set notation is used widely in mathematics and in this book it is employed where appropriate. A set is a general name for any collection of things or numbers. There must be a way of deciding whether any particul ...
... This chapter introduces set notation and discusses sets of numbers and their properties. Set notation is used widely in mathematics and in this book it is employed where appropriate. A set is a general name for any collection of things or numbers. There must be a way of deciding whether any particul ...
Table of Contents - Continental Press
... SAMPLE Travis has a 6-foot long rope. He ties a knot in the rope every ...
... SAMPLE Travis has a 6-foot long rope. He ties a knot in the rope every ...
An example of a computable absolutely normal number
... and using Lemma 4 we deduce µ ∆ ∩ cnbn < 21n = µ cnbn . Hence, the set ∆ does not cover the interval cnbn . There must be real numbers in the interval cnbn that belong to no interval of ∆. Theorem 7. The number ν is computable and absolutely normal. Proof. In our construction we need only to compute ...
... and using Lemma 4 we deduce µ ∆ ∩ cnbn < 21n = µ cnbn . Hence, the set ∆ does not cover the interval cnbn . There must be real numbers in the interval cnbn that belong to no interval of ∆. Theorem 7. The number ν is computable and absolutely normal. Proof. In our construction we need only to compute ...
Fractions Solutions
... (just divide by 1). But whether a number if rational depends on its value, not on the way it is written. What we’re saying is that in the case of fractions, we are dealing with a syntactic issue, and in case of rational numbers, a semantic issue, to borrow two terms from computer science. For comple ...
... (just divide by 1). But whether a number if rational depends on its value, not on the way it is written. What we’re saying is that in the case of fractions, we are dealing with a syntactic issue, and in case of rational numbers, a semantic issue, to borrow two terms from computer science. For comple ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.