Fortran 90 Control Structures
... zGiven a p positive integer, g , one can always y factorize it into prime factors. The following is an example: ...
... zGiven a p positive integer, g , one can always y factorize it into prime factors. The following is an example: ...
Computing Fibonacci Numbers Fast using the Chinese Remainder
... The nice, predictable form of the period yields an easy way to find the remainders r for the CRT. The first n terms of the sequence is simply the first n Fibonacci numbers and the next n terms is just the first sequence descending from n with an alternating sign. When n is even, the last few terms a ...
... The nice, predictable form of the period yields an easy way to find the remainders r for the CRT. The first n terms of the sequence is simply the first n Fibonacci numbers and the next n terms is just the first sequence descending from n with an alternating sign. When n is even, the last few terms a ...
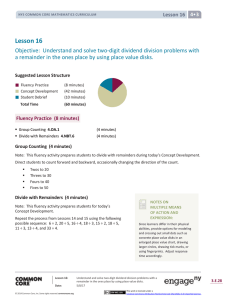
4 minutes
... How do we use multiplication and addition to check our quotient and remainder in division? Two times 3 is 6. Six plus 2 is 8. We multiply the quotient times the divisor and add the remainder. We multiply the number in each group by the number of groups and then add the remainder. ...
... How do we use multiplication and addition to check our quotient and remainder in division? Two times 3 is 6. Six plus 2 is 8. We multiply the quotient times the divisor and add the remainder. We multiply the number in each group by the number of groups and then add the remainder. ...
ppt
... another common use of hex numbers are to represent colours recall our discussion about colour models, in particular, the RGB (Red-Green-Blue) model a copy of the relevant slide from the Terminology III slides has been included here, for convenience ...
... another common use of hex numbers are to represent colours recall our discussion about colour models, in particular, the RGB (Red-Green-Blue) model a copy of the relevant slide from the Terminology III slides has been included here, for convenience ...
Word document
... (1/4s, 1/2s, 1/8s, 1/10s, 1/16s) using numbers, pictures (E.g. drawings or base ten blocks), and number lines. Order and compare fractions (1/4s, 1/2s, 1/8s, 1/10s, 1/16s)represented ...
... (1/4s, 1/2s, 1/8s, 1/10s, 1/16s) using numbers, pictures (E.g. drawings or base ten blocks), and number lines. Order and compare fractions (1/4s, 1/2s, 1/8s, 1/10s, 1/16s)represented ...
Book 1 - McGraw Hill Higher Education
... Copyright © 2010 The McGraw-Hill Companies, Inc. All rights reserved. No part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written consent of The McGraw-Hill Companies, Inc., including, but not limit ...
... Copyright © 2010 The McGraw-Hill Companies, Inc. All rights reserved. No part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written consent of The McGraw-Hill Companies, Inc., including, but not limit ...
Curriculum Unit Overview Tiffany Roth Curriculum Development
... KS2004.M.9-10.1.1 – BENCHMARK: Number Sense – The student demonstrates number sense for real numbers and algebraic expressions in a variety of situations. KS2004.M.9-10.1.1.K.1 – KBI: knows, explains, and uses equivalent representations for real numbers and algebraic expressions including integers, ...
... KS2004.M.9-10.1.1 – BENCHMARK: Number Sense – The student demonstrates number sense for real numbers and algebraic expressions in a variety of situations. KS2004.M.9-10.1.1.K.1 – KBI: knows, explains, and uses equivalent representations for real numbers and algebraic expressions including integers, ...
Problem Solving
... Can You Just Tell Me How Old Your Children Are! 11. A student asked his math teacher, “How many children do you have, and how old are they?” “I have 3 girls,” replied the teacher. “The product of their ages is 72, and the sum of their ages is the same as the room number of this classroom.” Knowing ...
... Can You Just Tell Me How Old Your Children Are! 11. A student asked his math teacher, “How many children do you have, and how old are they?” “I have 3 girls,” replied the teacher. “The product of their ages is 72, and the sum of their ages is the same as the room number of this classroom.” Knowing ...
Full text
... surprising, it is actually very natural as Benford’s law is equivalent to the logarithms of the set being equidistributed modulo 1. For more on Benford’s law see [15, 16, 21, 24], as well as [20] for a compilation of articles on its theory and applications. Obviously, we would not be discussing Benf ...
... surprising, it is actually very natural as Benford’s law is equivalent to the logarithms of the set being equidistributed modulo 1. For more on Benford’s law see [15, 16, 21, 24], as well as [20] for a compilation of articles on its theory and applications. Obviously, we would not be discussing Benf ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.