Maths Workshop - St Martin de Porres Catholic Primary School
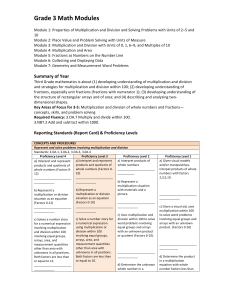
... I know the division facts for the 2 and 10 times table. Spring 1 I know the division facts for the 3 and 5 times table. Spring 2 I know number bonds to 20. Summer 1 I know 10 more and 10 less from a given number to 100. ...
... I know the division facts for the 2 and 10 times table. Spring 1 I know the division facts for the 3 and 5 times table. Spring 2 I know number bonds to 20. Summer 1 I know 10 more and 10 less from a given number to 100. ...
Information Encoding
... Step 5) If your result was less than 1000, form the 9’s complement again and add 1 and remember your result is negative else subtract 1000 ...
... Step 5) If your result was less than 1000, form the 9’s complement again and add 1 and remember your result is negative else subtract 1000 ...
PDF
... no finite amount of decimals in them suffices to give their exact values. Remark 2. In both of the above examples, no of the sequence members was equal to the limit, but it does not need always to be so; thus for example 1+(−1)n ...
... no finite amount of decimals in them suffices to give their exact values. Remark 2. In both of the above examples, no of the sequence members was equal to the limit, but it does not need always to be so; thus for example 1+(−1)n ...
2.5 Division of Integers
... 5 • x = !45 , thus x = !9 . Similarly, for 36 ÷ (!4) we have 36 ÷ (!4) = x , so !4 • x = 36 , and thus x = !9 . Thus one negative number results in a quotient which is negative. If we are dividing two negative numbers such as !28 ÷ (!7) , let !28 ÷ (!7) = x and so !7 • x = !28 , thus x = 4 . So divi ...
... 5 • x = !45 , thus x = !9 . Similarly, for 36 ÷ (!4) we have 36 ÷ (!4) = x , so !4 • x = 36 , and thus x = !9 . Thus one negative number results in a quotient which is negative. If we are dividing two negative numbers such as !28 ÷ (!7) , let !28 ÷ (!7) = x and so !7 • x = !28 , thus x = 4 . So divi ...
4.3 Dividing Fractions Example 1: Write the reciprocal of the
... Reciprocals are sometimes called multiplicative inverses. Example 1: Write the reciprocal of the following numbers. a) ...
... Reciprocals are sometimes called multiplicative inverses. Example 1: Write the reciprocal of the following numbers. a) ...
Chemistry 30
... Ionic compounds can be named using either of two similar methods. In order to name ionic compounds one must first understand how ionic compounds come to be. Ionic compounds are formed as a result of cations and anions which are attracted to each other because of their opposite charge and join in rat ...
... Ionic compounds can be named using either of two similar methods. In order to name ionic compounds one must first understand how ionic compounds come to be. Ionic compounds are formed as a result of cations and anions which are attracted to each other because of their opposite charge and join in rat ...
Arithmetic

Arithmetic or arithmetics (from the Greek ἀριθμός arithmos, ""number"") is the oldest and most elementary branch of mathematics. It consists of the study of numbers, especially the properties of the traditional operations between them—addition, subtraction, multiplication and division. Arithmetic is an elementary part of number theory, and number theory is considered to be one of the top-level divisions of modern mathematics, along with algebra, geometry, and analysis. The terms arithmetic and higher arithmetic were used until the beginning of the 20th century as synonyms for number theory and are sometimes still used to refer to a wider part of number theory.