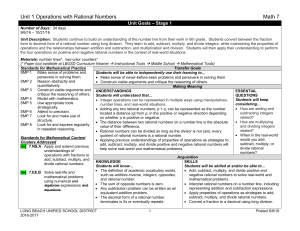
Lesson 1 - BGRS - Engaging Students
... In mathematics you can express the measures below sea level with a number called an integer. You will learn how to express numbers that are greater than and less than 0 using integers. An integer for the depth of this submarine is: -100 metres. This is “negative 100 metres” when you read it out loud ...
... In mathematics you can express the measures below sea level with a number called an integer. You will learn how to express numbers that are greater than and less than 0 using integers. An integer for the depth of this submarine is: -100 metres. This is “negative 100 metres” when you read it out loud ...
Exact Computer Calculations With Infinitely Repeating Decimals
... truncating of decimals produces approximations rather than exact results. However, terminating decimals allow for computers and calculators to produce exact mathematical calculations. This investigation demonstrates that any rational number may be converted into another base in which the bessimal wi ...
... truncating of decimals produces approximations rather than exact results. However, terminating decimals allow for computers and calculators to produce exact mathematical calculations. This investigation demonstrates that any rational number may be converted into another base in which the bessimal wi ...
P-adic number
In mathematics the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems. The extension is achieved by an alternative interpretation of the concept of ""closeness"" or absolute value. In particular, p-adic numbers have the interesting property that they are said to be close when their difference is divisible by a high power of p – the higher the power the closer they are. This property enables p-adic numbers to encode congruence information in a way that turns out to have powerful applications in number theory including, for example, in the famous proof of Fermat's Last Theorem by Andrew Wiles.p-adic numbers were first described by Kurt Hensel in 1897, though with hindsight some of Kummer's earlier work can be interpreted as implicitly using p-adic numbers. The p-adic numbers were motivated primarily by an attempt to bring the ideas and techniques of power series methods into number theory. Their influence now extends far beyond this. For example, the field of p-adic analysis essentially provides an alternative form of calculus.More formally, for a given prime p, the field Qp of p-adic numbers is a completion of the rational numbers. The field Qp is also given a topology derived from a metric, which is itself derived from the p-adic order, an alternative valuation on the rational numbers. This metric space is complete in the sense that every Cauchy sequence converges to a point in Qp. This is what allows the development of calculus on Qp, and it is the interaction of this analytic and algebraic structure which gives the p-adic number systems their power and utility.The p in p-adic is a variable and may be replaced with a prime (yielding, for instance, ""the 2-adic numbers"") or another placeholder variable (for expressions such as ""the ℓ-adic numbers""). The ""adic"" of ""p-adic"" comes from the ending found in words such as dyadic or triadic, and the p means a prime number.