Geometry Fall 2013 Topics
... f. Pythagorean Theorem and Its Converse [solving quadratic equations by factoring, completing the square, or using the Quadratic Formula (OPTIONAL)] g. Pythagorean Theorem (proof using areas of squares and triangles) (Ch. 8-2) h. Determining whether a triangle is obtuse, right, or acute (Ch. 8-3) i. ...
... f. Pythagorean Theorem and Its Converse [solving quadratic equations by factoring, completing the square, or using the Quadratic Formula (OPTIONAL)] g. Pythagorean Theorem (proof using areas of squares and triangles) (Ch. 8-2) h. Determining whether a triangle is obtuse, right, or acute (Ch. 8-3) i. ...
Lesson 9.1 and 9.2 - Crestwood Local Schools
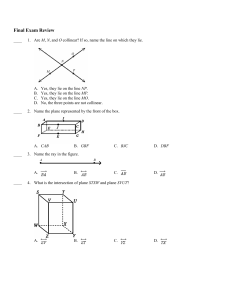
... You are looking directly down into a wooden crate. Name each of the following. a. four segments that intersect PT MP, OP, QT, ST b. three segments parallel to PT ...
... You are looking directly down into a wooden crate. Name each of the following. a. four segments that intersect PT MP, OP, QT, ST b. three segments parallel to PT ...
Unit 1 Conjectures
... Angle Bisector Conjecture: If a point is on the bisector of an angle, then it is __________________ from the sides of the angle. ...
... Angle Bisector Conjecture: If a point is on the bisector of an angle, then it is __________________ from the sides of the angle. ...
The Nine Point Circle
... ∠ HbHcHa = 180° – 2C Æ Oc lies on the same circle as the midpoints and feet of the altitudes of triangle ABC because HaHcHbOc is cyclic. This argument can be repeated for Oa and Ob. Also, Oa, Ob, and Oc are sometimes referred to as the midpoints of the segments from the orthocenter to the vertices, ...
... ∠ HbHcHa = 180° – 2C Æ Oc lies on the same circle as the midpoints and feet of the altitudes of triangle ABC because HaHcHbOc is cyclic. This argument can be repeated for Oa and Ob. Also, Oa, Ob, and Oc are sometimes referred to as the midpoints of the segments from the orthocenter to the vertices, ...