Full text
... Let us now consider the case in which the multipliers are 0, 1 and the basic sequence i s the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, • • ' , That this sequence gives complete r e p resentation i s not difficult to prove. In fact, the representation i s still complete if we e l i m inate the first ...
... Let us now consider the case in which the multipliers are 0, 1 and the basic sequence i s the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, • • ' , That this sequence gives complete r e p resentation i s not difficult to prove. In fact, the representation i s still complete if we e l i m inate the first ...
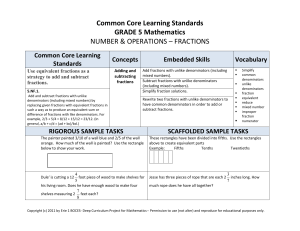
Math Scope and Sequence
... Using Geometry (with Assessments) Using Geometry: Pretest Area: Counting Square Units Calculating the Area of Rectangles and Squares Calculating the Area of Triangles Calculating the Volume of a Rectangular Prism Measurement (with Assessments) Measurement: Pretest Measuring Length: Metric Units Meas ...
... Using Geometry (with Assessments) Using Geometry: Pretest Area: Counting Square Units Calculating the Area of Rectangles and Squares Calculating the Area of Triangles Calculating the Volume of a Rectangular Prism Measurement (with Assessments) Measurement: Pretest Measuring Length: Metric Units Meas ...
Series-ous Escape
... • establishing that every next power is the sum of all before it and one more. Note in this example the powers of 2 begin at 2 so the general term is 2 less, not 1 less. Exercise 6 Teaching lessons preceeding this exercise could include:• modelling the multiples of the counting numbers Exercise 7 Te ...
... • establishing that every next power is the sum of all before it and one more. Note in this example the powers of 2 begin at 2 so the general term is 2 less, not 1 less. Exercise 6 Teaching lessons preceeding this exercise could include:• modelling the multiples of the counting numbers Exercise 7 Te ...
doc - Numeric
... Example: If you had 203, you would double the ones digit to get six, and subtract that from 20 to get 14. If you get an answer divisible by 7 (including zero), then the original number is divisible by seven. If you don't know the new number's divisibility, you can apply the rule again. Here is anoth ...
... Example: If you had 203, you would double the ones digit to get six, and subtract that from 20 to get 14. If you get an answer divisible by 7 (including zero), then the original number is divisible by seven. If you don't know the new number's divisibility, you can apply the rule again. Here is anoth ...
1) - Mu Alpha Theta
... Bradley the frog is jumping across a river. There are 50 lily pads spanning from one edge to the other as shown in the figure. Bradley wants to cross the river by following a certain pattern. He first makes 5 hops forward, then one backwards, then 5 forward again, then one backward, and so forth unt ...
... Bradley the frog is jumping across a river. There are 50 lily pads spanning from one edge to the other as shown in the figure. Bradley wants to cross the river by following a certain pattern. He first makes 5 hops forward, then one backwards, then 5 forward again, then one backward, and so forth unt ...
Fixed-Point Arithmetic: An Introduction
... rules and guidelines for the manipulation of these number representations using the common arithmetic and logical operations found in fixed-point DSPs and hardware components. While there is nothing particularly difficult about this subject, I found little documentation either in hardcopy or on the ...
... rules and guidelines for the manipulation of these number representations using the common arithmetic and logical operations found in fixed-point DSPs and hardware components. While there is nothing particularly difficult about this subject, I found little documentation either in hardcopy or on the ...