Subject Area: Math
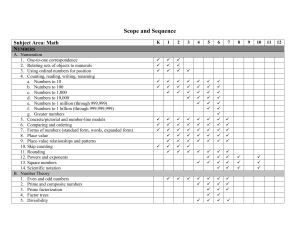
... Scope and Sequence Subject Area: Math NUMBERS A. Numeration 1. One-to-one correspondence 2. Relating sets of objects to numerals 3. Using ordinal numbers for position 4. Counting, reading, writing, renaming a. Numbers to 10 b. Numbers to 100 c. Numbers to 1,000 d. Numbers to 10,000 e. Numbers to 1 m ...
... Scope and Sequence Subject Area: Math NUMBERS A. Numeration 1. One-to-one correspondence 2. Relating sets of objects to numerals 3. Using ordinal numbers for position 4. Counting, reading, writing, renaming a. Numbers to 10 b. Numbers to 100 c. Numbers to 1,000 d. Numbers to 10,000 e. Numbers to 1 m ...
Counting - H-SC
... Inductive case: Suppose that the statement is true when n = k, for some integer k 0. Consider a set of k + 1 elements. If r = 0, then there is only one 0-combination, the null set, and ...
... Inductive case: Suppose that the statement is true when n = k, for some integer k 0. Consider a set of k + 1 elements. If r = 0, then there is only one 0-combination, the null set, and ...
Counting Subsets of a Set
... Counting r-Combinations So let r be any number between 0 and k + 1 (0 < r < k + 1). Select an arbitrary element a from the set. For each r-combination of the k + 1 elements, a is either a member or not a member. We will count the r-combinations for which a is a member and then count the rcomb ...
... Counting r-Combinations So let r be any number between 0 and k + 1 (0 < r < k + 1). Select an arbitrary element a from the set. For each r-combination of the k + 1 elements, a is either a member or not a member. We will count the r-combinations for which a is a member and then count the rcomb ...
Solutions for the first week`s homework Math 131
... obvious. Note that 112 = 121 and 1112 = 12 321. This pattern will break after the central digit is 9. Why? Note that computing 101 010 1012 with common desktop computers may produce 10 203 040 504 030 200. The last digit falls off the end of how computers represent floating-point numbers. Computing ...
... obvious. Note that 112 = 121 and 1112 = 12 321. This pattern will break after the central digit is 9. Why? Note that computing 101 010 1012 with common desktop computers may produce 10 203 040 504 030 200. The last digit falls off the end of how computers represent floating-point numbers. Computing ...
SigFig ppt - Ms. Dougalas
... given so that it will cancel. 4. Put a unit on the opposite side that will be the new unit. If you don’t know a conversion between those units directly, use one that you do know that is a step toward the one you want at the end. 5. Insert the numbers on the conversion so that the top and the bottom ...
... given so that it will cancel. 4. Put a unit on the opposite side that will be the new unit. If you don’t know a conversion between those units directly, use one that you do know that is a step toward the one you want at the end. 5. Insert the numbers on the conversion so that the top and the bottom ...
Full text
... and such that there are at least m - 1 zeros between any two l's in this representation of Z. Hence, for n > 1, ^ + x is the number of binary strings of length n - 1 having this property. For n = 2 5 we again get the property that there are no adjacent ones in the binary representation, An interesti ...
... and such that there are at least m - 1 zeros between any two l's in this representation of Z. Hence, for n > 1, ^ + x is the number of binary strings of length n - 1 having this property. For n = 2 5 we again get the property that there are no adjacent ones in the binary representation, An interesti ...