DesignCon 2008 Solutions for Causal Modeling and A Technique
... modeling. When working in the multi-GHz frequency range, this modeling typically requires full-wave electromagnetic analysis. Many engineers work diligently to learn complicated 3D modeling tools so that they can accurately represent physical geometries and electrical boundary conditions. However, p ...
... modeling. When working in the multi-GHz frequency range, this modeling typically requires full-wave electromagnetic analysis. Many engineers work diligently to learn complicated 3D modeling tools so that they can accurately represent physical geometries and electrical boundary conditions. However, p ...
Mitigation and Analysis of Very Fast Transient over
... which are dangerous for the transformer and the system insulation because of their short rise time. Under special circumstances the terminal over voltages can arise close to the transformer. The suppression of VFTO is very important in GIS systems. In this a 245KV gas insulated substation has been c ...
... which are dangerous for the transformer and the system insulation because of their short rise time. Under special circumstances the terminal over voltages can arise close to the transformer. The suppression of VFTO is very important in GIS systems. In this a 245KV gas insulated substation has been c ...
Formally Verifying Transfer Functions of Analog Circuits using
... signals in a wide range of applications. Functional verification of these analog circuits used independently or as a part of an embedded system is of paramount importance given the safety-critical nature of hardware applications these days. The goal of the functional verification of an analog circu ...
... signals in a wide range of applications. Functional verification of these analog circuits used independently or as a part of an embedded system is of paramount importance given the safety-critical nature of hardware applications these days. The goal of the functional verification of an analog circu ...
JRRP2014_Guccione_Bornstein - MD-SOAR
... the Library of Congress where I located a valuable compilation of primary sources annotated by the Dutch mathematician Dirk Van Dalen. I also reached out to both Professor Robert Lewand and Professor Justin Brody in the Math and Computer Science department to guide my research. After gaining a solid ...
... the Library of Congress where I located a valuable compilation of primary sources annotated by the Dutch mathematician Dirk Van Dalen. I also reached out to both Professor Robert Lewand and Professor Justin Brody in the Math and Computer Science department to guide my research. After gaining a solid ...
Z35149151
... transient signal, simultaneously both in time and frequency domain. MATLAB software is used to simulate different operating and fault conditions on high voltage transmission line, namely single phase to ground fault, line to line fault, double line to ground and three phase short circuit. Keywords- ...
... transient signal, simultaneously both in time and frequency domain. MATLAB software is used to simulate different operating and fault conditions on high voltage transmission line, namely single phase to ground fault, line to line fault, double line to ground and three phase short circuit. Keywords- ...
unitary extensions of isometries, generalized interpolation and band
... for every k > 0, and the corresponding solution of a generalized interpolation problem can be considered as the maximum entropy solution. There exists a bijection between the set of all the Nagy–Foiaş intertwining liftings of a commutant and a set of choice sequences (see [FF] and references therei ...
... for every k > 0, and the corresponding solution of a generalized interpolation problem can be considered as the maximum entropy solution. There exists a bijection between the set of all the Nagy–Foiaş intertwining liftings of a commutant and a set of choice sequences (see [FF] and references therei ...
Chapter 4 - UniMAP Portal
... In this Chapter 4 we are considering the continuous-time signal and system representation based on complex exponential signals. The Laplace transform can be used to analyze a large class of continuous-time problems involving signal that are not absolutely integrable, such as impulse response of ...
... In this Chapter 4 we are considering the continuous-time signal and system representation based on complex exponential signals. The Laplace transform can be used to analyze a large class of continuous-time problems involving signal that are not absolutely integrable, such as impulse response of ...
The Fourier transform of e
... fˆa (w) = e−kw in which k is a positive constant. This is highly remarkable and does not hold in the general case. On the other hand, other functions do exist for which the Fourier transform is of the same form as the original function, meaning that fa (x) is not entirely exceptional in this respect ...
... fˆa (w) = e−kw in which k is a positive constant. This is highly remarkable and does not hold in the general case. On the other hand, other functions do exist for which the Fourier transform is of the same form as the original function, meaning that fa (x) is not entirely exceptional in this respect ...
Fault Detection in Induction Machine by Application
... Applying this relationship, the result is a complex signal with a real part and an imaginary that allows writing the previous equation as: ...
... Applying this relationship, the result is a complex signal with a real part and an imaginary that allows writing the previous equation as: ...
Axiomatizing Metatheory: A Fregean Perspective on Independence
... We now return to our question: Is it possible to prove the independence of a real axiom from a group of real axioms? This leads to the further question: How can one prove the independence of a thought from a group of thoughts? First of all, it may be noted that with this question we enter into a rea ...
... We now return to our question: Is it possible to prove the independence of a real axiom from a group of real axioms? This leads to the further question: How can one prove the independence of a thought from a group of thoughts? First of all, it may be noted that with this question we enter into a rea ...
Introduction
... The main goal of Chapter 5, by C. Walsh, is to give an explicit description of the horofunction boundary of a Hilbert geometry. This notion is based on ideas that go back to Busemann but which were formally introduced by Gromov. The results in this chapter are mainly due to Walsh. Walsh gives a sket ...
... The main goal of Chapter 5, by C. Walsh, is to give an explicit description of the horofunction boundary of a Hilbert geometry. This notion is based on ideas that go back to Busemann but which were formally introduced by Gromov. The results in this chapter are mainly due to Walsh. Walsh gives a sket ...
ME451 - MSU College of Engineering
... If U(s)=1/s, the unit step input function, then Y(s)=H(s)/s is the step response The magnitude and phase shift of the response to a sinusoid at frequency is given by the magnitude and phase of the complex number Impulse: Unit step: ...
... If U(s)=1/s, the unit step input function, then Y(s)=H(s)/s is the step response The magnitude and phase shift of the response to a sinusoid at frequency is given by the magnitude and phase of the complex number Impulse: Unit step: ...
CHAPTER 17
... 2) If the one-sided Laplace transform of f(t) exists and all the poles of F(s) lies in the left half of the s plane, F(s) may be used to find F(). 3) If f(t) is a constant, a signum function, a step function, or a sinusoidal function, the Fourier transform is found by using a limit process. © 2008 ...
... 2) If the one-sided Laplace transform of f(t) exists and all the poles of F(s) lies in the left half of the s plane, F(s) may be used to find F(). 3) If f(t) is a constant, a signum function, a step function, or a sinusoidal function, the Fourier transform is found by using a limit process. © 2008 ...
Classroom Note Fourier Method for Laplace Transform Inversion †
... (see [1, 5]). This has the advantage of removing quadrature errors from the coefficients in the expansion (2.4) which are amplified by small eigenvalues. ...
... (see [1, 5]). This has the advantage of removing quadrature errors from the coefficients in the expansion (2.4) which are amplified by small eigenvalues. ...
t - ÉTS
... process. Having gained confidence with Laplace transforms techniques, we solve by hand without numeric values the ODE We find the following solution: ...
... process. Having gained confidence with Laplace transforms techniques, we solve by hand without numeric values the ODE We find the following solution: ...
Key_P1 - Weber State University
... with time-delay (time delay t=phase ϕ/(360*frequency f)). Linear phase indicates that there is going to be same time delay for all the frequencies, since t will be the same. This allows for all the harmonics to be delayed by the same amount 360 f which is important for processing an input ...
... with time-delay (time delay t=phase ϕ/(360*frequency f)). Linear phase indicates that there is going to be same time delay for all the frequencies, since t will be the same. This allows for all the harmonics to be delayed by the same amount 360 f which is important for processing an input ...
Chapter 7 : Existence Theorems
... Chapter 7 : Existence Theorems 7.2 : A Hilbert Space Approach The completion of V If V is an inner product space that is not complete, then V can be embedded as a dense subset of a Hilbert space H. This means that there is a Hilbert space such that V inside H. We call such H the completion of V. ...
... Chapter 7 : Existence Theorems 7.2 : A Hilbert Space Approach The completion of V If V is an inner product space that is not complete, then V can be embedded as a dense subset of a Hilbert space H. This means that there is a Hilbert space such that V inside H. We call such H the completion of V. ...
Document
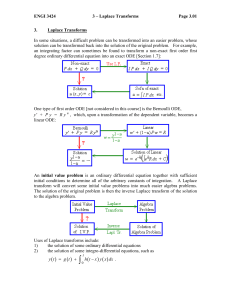
... Reminder: Laplace Transform The continuous time Laplace transform is important for two reasons: • It can be considered as a Fourier transform when the signals had infinite energy • It decomposes a signal x(t) in terms of its basis functions est, which are only altered by magnitude/phase when passed ...
... Reminder: Laplace Transform The continuous time Laplace transform is important for two reasons: • It can be considered as a Fourier transform when the signals had infinite energy • It decomposes a signal x(t) in terms of its basis functions est, which are only altered by magnitude/phase when passed ...
Mathematical Models of Systems
... A mathematical model is a set of equations (usually differential equations) that represents the dynamics of systems. In practice, the complexity of the system requires some assumptions in the determination model. The equations of the mathematical model may be solved using mathematical tools such as ...
... A mathematical model is a set of equations (usually differential equations) that represents the dynamics of systems. In practice, the complexity of the system requires some assumptions in the determination model. The equations of the mathematical model may be solved using mathematical tools such as ...
solution of heat equation on a semi infinite line using
... The French physicist J. Fourier announced in his work on heat conduction that an “arbitrary function” could be expanded in a series of sinusoidal functions. The Fourier integral was introduced by Fourier as an attempt to generalize his results from finite intervals to infinite interval. The Fourier ...
... The French physicist J. Fourier announced in his work on heat conduction that an “arbitrary function” could be expanded in a series of sinusoidal functions. The Fourier integral was introduced by Fourier as an attempt to generalize his results from finite intervals to infinite interval. The Fourier ...
Nyquist–Shannon sampling theorem
... In this analysis, the Laplace transform is often interpreted as a transformation from the time-domain, in which inputs and outputs are functions of time, to the frequency-domain, where the same inputs and outputs are functions of complex angular frequency, in radians per unit time. Given a simple ma ...
... In this analysis, the Laplace transform is often interpreted as a transformation from the time-domain, in which inputs and outputs are functions of time, to the frequency-domain, where the same inputs and outputs are functions of complex angular frequency, in radians per unit time. Given a simple ma ...
and wavelets
... that one signal is broken down into many lower resolution components. This is called the wavelet decomposition tree. For detection of transients a multi-resolution analysis tree based on wavelets has been applied. Every one of wavelet transform subbands is reconstructed separately from each other, s ...
... that one signal is broken down into many lower resolution components. This is called the wavelet decomposition tree. For detection of transients a multi-resolution analysis tree based on wavelets has been applied. Every one of wavelet transform subbands is reconstructed separately from each other, s ...
Hilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u(t), and produces a function, H(u)(t), with the same domain. The Hilbert transform is important in the field of signal processing where it is used to derive the analytic representation of a signal u(t). This means that the real signal u(t) is extended into the complex plane such that it satisfies the Cauchy-Riemann equations.For example, the Hilbert transform leads to the harmonic conjugate of a given function in Fourier analysis, aka harmonic analysis. Equivalently, it is an example of a singular integral operator and of a Fourier multiplier.The Hilbert transform was originally defined for periodic functions, or equivalently for functions on the circle, in which case it is given by convolution with the Hilbert kernel. More commonly, however, the Hilbert transform refers to a convolution with the Cauchy kernel, for functions defined on the real line R (the boundary of the upper half-plane). The Hilbert transform is closely related to the Paley–Wiener theorem, another result relating holomorphic functions in the upper half-plane and Fourier transforms of functions on the real line.The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the Riemann–Hilbert problem for holomorphic functions.