On the topological Hochschild homology of bu. I.
... T HH(`) and use it to find the E2 term of the ASS converging to π∗ (T HH(`); Z/p). This section also contains a quick calculation, which was pointed out to us by Larry Smith and Andy Baker, of the homotopy groups of T HH(BP ), where BP is the BrownPeterson summand of complex cobordism. In Section 5 ...
... T HH(`) and use it to find the E2 term of the ASS converging to π∗ (T HH(`); Z/p). This section also contains a quick calculation, which was pointed out to us by Larry Smith and Andy Baker, of the homotopy groups of T HH(BP ), where BP is the BrownPeterson summand of complex cobordism. In Section 5 ...
MORE ON THE SYLOW THEOREMS 1. Introduction
... Several alternative proofs of the Sylow theorems are collected here. Section 2 has a proof of Sylow I by Sylow, Section 3 has a proof of Sylow I by Frobenius, and Section 4 has an extension of Sylow I and II to p-subgroups due to Sylow. Section 5 discusses some history related to the Sylow theorems ...
... Several alternative proofs of the Sylow theorems are collected here. Section 2 has a proof of Sylow I by Sylow, Section 3 has a proof of Sylow I by Frobenius, and Section 4 has an extension of Sylow I and II to p-subgroups due to Sylow. Section 5 discusses some history related to the Sylow theorems ...
Reduced coproducts of compact Hausdorff spaces
... first question is no. For let X = 2' = {0, 1}' be the countable Tichonov power of the two-point discrete space, let Y = 2"1, and let 9 be a free ultrafilter on a countable set. Then IH XI= c = exp(o), and IH YI = exp(w) = exp(c) > c. However B(X) and B(Y), being atomless Boolean algebras, are elemen ...
... first question is no. For let X = 2' = {0, 1}' be the countable Tichonov power of the two-point discrete space, let Y = 2"1, and let 9 be a free ultrafilter on a countable set. Then IH XI= c = exp(o), and IH YI = exp(w) = exp(c) > c. However B(X) and B(Y), being atomless Boolean algebras, are elemen ...
3. Abstract Boolean Algebras 3.1. Abstract Boolean Algebra.
... (x1 , x2 , x3 , . . . , xk )·“one” = (x1 , x2 , x3 , . . . , xk ) and (x1 ·x1 , x2 ·x2 , x3 ·x3 , . . . , xk ·xk ). Notice that the ordered k-tuple of all 1’s satisfies these properties, so the “one” element is (1, 1, 1, . . . , 1). BOOL(k) defined to be the set of all Boolean functions of degree k ...
... (x1 , x2 , x3 , . . . , xk )·“one” = (x1 , x2 , x3 , . . . , xk ) and (x1 ·x1 , x2 ·x2 , x3 ·x3 , . . . , xk ·xk ). Notice that the ordered k-tuple of all 1’s satisfies these properties, so the “one” element is (1, 1, 1, . . . , 1). BOOL(k) defined to be the set of all Boolean functions of degree k ...
A conjecture on the Hall topology for the free group - LaCIM
... Proof. Let Sf be the class of all subsets of F{A) which are a finite union of sets where geF(A) and Gx,...,Gr are finitely generated of the form gG1G2...Gr, subgroups of F\A). Every finitely generated group is rational, by Proposition 2.1, and thus every element of Sf is rational. Since a finite set ...
... Proof. Let Sf be the class of all subsets of F{A) which are a finite union of sets where geF(A) and Gx,...,Gr are finitely generated of the form gG1G2...Gr, subgroups of F\A). Every finitely generated group is rational, by Proposition 2.1, and thus every element of Sf is rational. Since a finite set ...
Part IX. Factorization
... Note. We normally think of the Fundamental Theorem of Arithmetic as stating that every natural number can be uniquely written as a product of primes. The units in Z are 1 and −1 and the irreducibles in Z are the positive primes and the negative primes. So the only associate of a prime is its negativ ...
... Note. We normally think of the Fundamental Theorem of Arithmetic as stating that every natural number can be uniquely written as a product of primes. The units in Z are 1 and −1 and the irreducibles in Z are the positive primes and the negative primes. So the only associate of a prime is its negativ ...
Some Generalizations of Mulit-Valued Version of
... (resp. lower semi-continuous and continuous) if Q + (U ) (resp. Q − (U ) and Q −1 (U )) is open set in E 1 for every open subset U of E 2 . In what follows,we confine ourselves only to the fixed point theory related to upper semicontinuous multi-valued mappings in Banach spaces. The first fixed poin ...
... (resp. lower semi-continuous and continuous) if Q + (U ) (resp. Q − (U ) and Q −1 (U )) is open set in E 1 for every open subset U of E 2 . In what follows,we confine ourselves only to the fixed point theory related to upper semicontinuous multi-valued mappings in Banach spaces. The first fixed poin ...
MATH 436 Notes: Homomorphisms.
... and f1 = 1Z it follows that θ is a homomorphism of monoids. It is trivial to check that it is a bijection and so induces an isomorphism between (Z, ·) and End((Z, +)). This completes the proof. The following is an important concept for homomorphisms: Definition 1.11. If f : G → H is a homomorphism o ...
... and f1 = 1Z it follows that θ is a homomorphism of monoids. It is trivial to check that it is a bijection and so induces an isomorphism between (Z, ·) and End((Z, +)). This completes the proof. The following is an important concept for homomorphisms: Definition 1.11. If f : G → H is a homomorphism o ...
Determination of the Differentiably Simple Rings with a
... always assume that K is associative with a unit elementacting unitallyon the algebra. Jacobsonnoted(at least in a special case, see [16]) the followingclass of simple rings A which are not simple: A is the examples of differentiably groupring SG whereS is a simpleringof primecharacteristicp and G # ...
... always assume that K is associative with a unit elementacting unitallyon the algebra. Jacobsonnoted(at least in a special case, see [16]) the followingclass of simple rings A which are not simple: A is the examples of differentiably groupring SG whereS is a simpleringof primecharacteristicp and G # ...
On the existence of normal subgroups of prime index - Rose
... implies that G21 × G22 ⊆ (G1 × G2 )2 . So the two sets are indeed equal. In order to prove the main theorem of this section we rely on the fundamental theorem for finite abelian groups. Theorem 3.4. (Fundamental Theorem for Finite Abelian Group) Any finite abelian group is isomorphic to a direct sum ...
... implies that G21 × G22 ⊆ (G1 × G2 )2 . So the two sets are indeed equal. In order to prove the main theorem of this section we rely on the fundamental theorem for finite abelian groups. Theorem 3.4. (Fundamental Theorem for Finite Abelian Group) Any finite abelian group is isomorphic to a direct sum ...
Group Theory
... Let (G, ?) be a group structure and let S be a subset of G. We say that S is a subgroup of G if (S, ?) is a group structure in its own right. Note that S is a subgroup of G iff (1) (Binary Structure) ab ∈ S for every a, b ∈ S. (2) (Existence of Identity) There exists e0 ∈ S such that e0 a = a = ae0 ...
... Let (G, ?) be a group structure and let S be a subset of G. We say that S is a subgroup of G if (S, ?) is a group structure in its own right. Note that S is a subgroup of G iff (1) (Binary Structure) ab ∈ S for every a, b ∈ S. (2) (Existence of Identity) There exists e0 ∈ S such that e0 a = a = ae0 ...
Subgroups of Finite Index in Profinite Groups
... s for which g1 , . . . , gr ∈ Prs (X). Finally, set m = s + t. Then if g ∈ G, we can write g = gi u for some gi ∈ {g1 , . . . , gr } and u ∈ U . Since gi ∈ Prs (X) and u ∈ Prt (X), we see that we can write g as a combination of m members of X, as claimed. ...
... s for which g1 , . . . , gr ∈ Prs (X). Finally, set m = s + t. Then if g ∈ G, we can write g = gi u for some gi ∈ {g1 , . . . , gr } and u ∈ U . Since gi ∈ Prs (X) and u ∈ Prt (X), we see that we can write g as a combination of m members of X, as claimed. ...
A FIVE ELEMENT BASIS FOR THE UNCOUNTABLE LINEAR
... Theorem 1.2. [19] There is a set of reals X of cardinality continuum such that if f ⊆ X 2 is a continuous injective function, then f differs from the identity function on a set of cardinality less than continuum. From this it is routine to prove that under the Continuum Hypothesis there is no basis ...
... Theorem 1.2. [19] There is a set of reals X of cardinality continuum such that if f ⊆ X 2 is a continuous injective function, then f differs from the identity function on a set of cardinality less than continuum. From this it is routine to prove that under the Continuum Hypothesis there is no basis ...
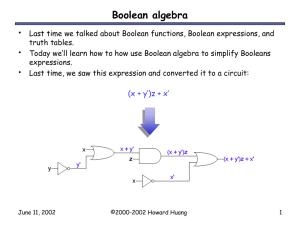
Boolean Algebra
... – “It is raining or it is not raining” is always true (x + x’ = 1) – “It is raining and it is not raining” can never be true (x x’ = 0) – “I am not not handsome” means “I am handsome” ((x’)’ = x) ...
... – “It is raining or it is not raining” is always true (x + x’ = 1) – “It is raining and it is not raining” can never be true (x x’ = 0) – “I am not not handsome” means “I am handsome” ((x’)’ = x) ...