Lesson 2.5
... Prentice Hall Foundations Geometry • Teaching Resources Copyright © by Pearson Education, Inc., or its affiliates. All Rights Reserved. ...
... Prentice Hall Foundations Geometry • Teaching Resources Copyright © by Pearson Education, Inc., or its affiliates. All Rights Reserved. ...
2-5 Practice
... Prentice Hall Foundations Geometry • Teaching Resources Copyright © by Pearson Education, Inc., or its affiliates. All Rights Reserved. ...
... Prentice Hall Foundations Geometry • Teaching Resources Copyright © by Pearson Education, Inc., or its affiliates. All Rights Reserved. ...
Writing Equivalent Expressions
... 20. Writing to Explain Eliot uses the Distributive Property to write an equivalent expression for 7(3x 1 4). He writes 21x 1 4. Emma notices that Eliot made a mistake. How could Emma explain to Eliot where he went wrong? What is the correct equivalent expression? ...
... 20. Writing to Explain Eliot uses the Distributive Property to write an equivalent expression for 7(3x 1 4). He writes 21x 1 4. Emma notices that Eliot made a mistake. How could Emma explain to Eliot where he went wrong? What is the correct equivalent expression? ...
Group Activity 2 - Georgia College Faculty Websites
... that every element is its own inverse. In fact, it’s abelian! c. To what group from Test 2 is G/H isomorphic? S. This group is isomorphic to the so-called Klein four group. It’s the group on exam two that is not Z4 with operation of addition. 3. Suppose φ : G → K is a group homomorphism. Prove that ...
... that every element is its own inverse. In fact, it’s abelian! c. To what group from Test 2 is G/H isomorphic? S. This group is isomorphic to the so-called Klein four group. It’s the group on exam two that is not Z4 with operation of addition. 3. Suppose φ : G → K is a group homomorphism. Prove that ...
Activity: The Distributive Law and Factoring
... Factoring Why do we factor? One reason that we factor is that an equation such as x2 − 2x + 3 = 0 can be solved by factoring as (x − 3)(x + 1) = 0 and then appealing to the fact that if a and b are real numbers and ab = 0, then either a = 0 or b = 0. So, in the example, either x − 3 = 0 or x + 1 = 0 ...
... Factoring Why do we factor? One reason that we factor is that an equation such as x2 − 2x + 3 = 0 can be solved by factoring as (x − 3)(x + 1) = 0 and then appealing to the fact that if a and b are real numbers and ab = 0, then either a = 0 or b = 0. So, in the example, either x − 3 = 0 or x + 1 = 0 ...
Lecture 7
... Proof (of Theorem). The key ideas of the proof are: ‚ #E1 “ #E2 “ pn for some prime p and n P N. Thus they both are finite extensions of the prime field Zp . ‚ Let E1 “ Zp pαq so E1 – Zp rxs{xf y where f “ irrpα, Zp q. n ‚ Since every element of E1 is a root of xp ´ x, it follows that f is a factor ...
... Proof (of Theorem). The key ideas of the proof are: ‚ #E1 “ #E2 “ pn for some prime p and n P N. Thus they both are finite extensions of the prime field Zp . ‚ Let E1 “ Zp pαq so E1 – Zp rxs{xf y where f “ irrpα, Zp q. n ‚ Since every element of E1 is a root of xp ´ x, it follows that f is a factor ...
Cauchy`s Theorem in Group Theory
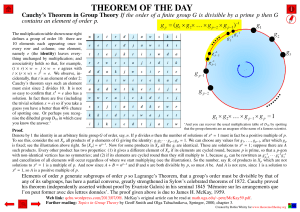
... Cauchy’s Theorem in Group Theory If the order of a finite group G is divisible by a prime p then G contains an element of order p. The multiplication table shown near right defines a group of order 10: there are 10 elements each appearing once in every row and column; one element, namely e (the iden ...
... Cauchy’s Theorem in Group Theory If the order of a finite group G is divisible by a prime p then G contains an element of order p. The multiplication table shown near right defines a group of order 10: there are 10 elements each appearing once in every row and column; one element, namely e (the iden ...