What is a Triangle?
... makes up the triangle that we want to cut out and the other region the leftover area of the paper not making up the triangle. Therefore, cutting along that ...
... makes up the triangle that we want to cut out and the other region the leftover area of the paper not making up the triangle. Therefore, cutting along that ...
maths powerpoint triangle investigation
... the length and width of the room. They remember that the area of the sitting room is 32m² and the room is not square, what is the length and width of Amardeep and Rajvi’s sitting room? ...
... the length and width of the room. They remember that the area of the sitting room is 32m² and the room is not square, what is the length and width of Amardeep and Rajvi’s sitting room? ...
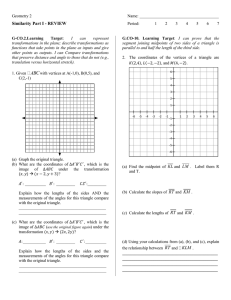
Geometry 2 Name: Similarity Part I - REVIEW Period: 1 2 3 4 5 6 7 G
... represent transformations in the plane; describe transformations as functions that take points in the plane as inputs and give other points as outputs. I can Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). ...
... represent transformations in the plane; describe transformations as functions that take points in the plane as inputs and give other points as outputs. I can Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). ...
Chapter 4 Review PowerPoint
... Our section was about the vocabulary that we have learned from the section. We had to fill in the blanks in the sentence that described the words. ...
... Our section was about the vocabulary that we have learned from the section. We had to fill in the blanks in the sentence that described the words. ...
2013 Student Delegates Statewide ______ Solutions
... 10. (C) Draw a chord passing through O and P. The point P splits this chord into segments of length r + OP and r – OP. By the Power of a Point theorem for intersecting chords (or using similar triangles), we have (AP)(PB) = (r + OP)(r – OP) = r2 – OP2, so (6)(4) = r2 – 22, so r2 = 28. Thus the area ...
... 10. (C) Draw a chord passing through O and P. The point P splits this chord into segments of length r + OP and r – OP. By the Power of a Point theorem for intersecting chords (or using similar triangles), we have (AP)(PB) = (r + OP)(r – OP) = r2 – OP2, so (6)(4) = r2 – 22, so r2 = 28. Thus the area ...
Incircle and excircles of a triangle
Incircle redirects here. For incircles of non-triangle polygons, see Tangential quadrilateral or Tangential polygon.In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is called the triangle's incenter.An excircle or escribed circle of the triangle is a circle lying outside the triangle, tangent to one of its sides and tangent to the extensions of the other two. Every triangle has three distinct excircles, each tangent to one of the triangle's sides.The center of the incircle, called the incenter, can be found as the intersection of the three internal angle bisectors. The center of an excircle is the intersection of the internal bisector of one angle (at vertex A, for example) and the external bisectors of the other two. The center of this excircle is called the excenter relative to the vertex A, or the excenter of A. Because the internal bisector of an angle is perpendicular to its external bisector, it follows that the center of the incircle together with the three excircle centers form an orthocentric system.Polygons with more than three sides do not all have an incircle tangent to all sides; those that do are called tangential polygons. See also Tangent lines to circles.