MEM12024A
... The laws protecting the Health and Safety of people at work apply to learners who attend TAFE Colleges, either part time or full time. These laws emphasise the need to take reasonable steps to eliminate or control risk at work (this includes a TAFE College). TAFE NSW has the responsibility for the c ...
... The laws protecting the Health and Safety of people at work apply to learners who attend TAFE Colleges, either part time or full time. These laws emphasise the need to take reasonable steps to eliminate or control risk at work (this includes a TAFE College). TAFE NSW has the responsibility for the c ...
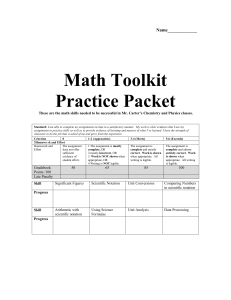
Math Toolkit Practice Packet
... How do we calculate standard deviation? There are 5 men. In statistical terms this means we have a population of 5. If we know the mass of each man, we use the standard deviation equation for the entire population: ...
... How do we calculate standard deviation? There are 5 men. In statistical terms this means we have a population of 5. If we know the mass of each man, we use the standard deviation equation for the entire population: ...
6 - Computer Science Division
... These can be done by using the Extended Euclidean Algorithm. Given r= n0, s= n1, or any 2 relatively prime numbers, EEA computes a, b such that a*r+b*s=1 = gcd(r,s) Look at this equation mod s: b*s is 0 (s is 0 mod s) and so we have a solution a*r=1 and hence a = inverse of r mod s. That’s what we w ...
... These can be done by using the Extended Euclidean Algorithm. Given r= n0, s= n1, or any 2 relatively prime numbers, EEA computes a, b such that a*r+b*s=1 = gcd(r,s) Look at this equation mod s: b*s is 0 (s is 0 mod s) and so we have a solution a*r=1 and hence a = inverse of r mod s. That’s what we w ...
36(2)
... Thus, all square sub-arrays of the Pascal array with top-left comer {§} = 1 are unimodular. Property 5 (Generalizations): The derivations of Properties 1-4 rely (if at all) only on the lefthand (p = -l) zero boundary conditions. They thus apply to the Pascal array generalized by arbitrary top-row en ...
... Thus, all square sub-arrays of the Pascal array with top-left comer {§} = 1 are unimodular. Property 5 (Generalizations): The derivations of Properties 1-4 rely (if at all) only on the lefthand (p = -l) zero boundary conditions. They thus apply to the Pascal array generalized by arbitrary top-row en ...
Divisibility Rules - York Catholic District School Board
... the last digit, double it, and subtract it from the rest of the number; if the answer is divisible by 7 (including 0), then the number is also. Ex: 672 (Double 2 is 4, 67- 4 = 63, and 63 ÷ 7 = 9) Yes {OR continue: double 3 = 6. 6 – 6 = 0) 905 (Double 5 is 10, 90 - 10 = 80, and 80 ÷ 7= 11 3/7) No Ex: ...
... the last digit, double it, and subtract it from the rest of the number; if the answer is divisible by 7 (including 0), then the number is also. Ex: 672 (Double 2 is 4, 67- 4 = 63, and 63 ÷ 7 = 9) Yes {OR continue: double 3 = 6. 6 – 6 = 0) 905 (Double 5 is 10, 90 - 10 = 80, and 80 ÷ 7= 11 3/7) No Ex: ...
Full text
... The literature devoted to this topic has become quite extensive. This seems in part to be due to the ease with which the question can be posed, particularly in the case of vectors in Z4 . For example, by experimenting with a variety of different vectors (a, b, c, d) ∈ Z4 , one will likely find that ...
... The literature devoted to this topic has become quite extensive. This seems in part to be due to the ease with which the question can be posed, particularly in the case of vectors in Z4 . For example, by experimenting with a variety of different vectors (a, b, c, d) ∈ Z4 , one will likely find that ...
Lesson # 18 Aim: How do we complete the square? - mvb-math
... example, 5 < x + 3 < 10 or -1 < 3x < 5. You solve them exactly the same way you solve the linear inequalities shown above, except you do the steps to three "sides" (or parts) instead of only two. Example 9: Solve, write your answer in interval notation and graph the solution set: This is an example ...
... example, 5 < x + 3 < 10 or -1 < 3x < 5. You solve them exactly the same way you solve the linear inequalities shown above, except you do the steps to three "sides" (or parts) instead of only two. Example 9: Solve, write your answer in interval notation and graph the solution set: This is an example ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.