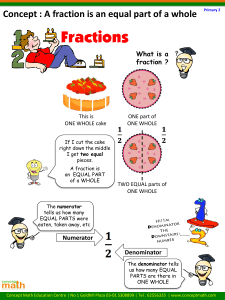
FACTOR POWER POINT by Jessa
... The first term in both sets of brackets, must multiply to get the first term. (3x )(3x ) Because it is a perfect square, the first numbers will be equal to each other. c) The second term in each bracket must also multiply to get the second term. (3x 4y)(3x 4y) d) Put a positive sign in one bracket, ...
... The first term in both sets of brackets, must multiply to get the first term. (3x )(3x ) Because it is a perfect square, the first numbers will be equal to each other. c) The second term in each bracket must also multiply to get the second term. (3x 4y)(3x 4y) d) Put a positive sign in one bracket, ...
Approximate Error
... - However, we always have to stop at a finite value of n=N. The truncation error is the difference between G(N) and G(∞). ...
... - However, we always have to stop at a finite value of n=N. The truncation error is the difference between G(N) and G(∞). ...
The Foundations: Logic and Proofs
... and B, at least three pies are thrown at A and B, and at most (2k + 3) − 3 = 2k pies are thrown at the remaining 2k + 1 people. This guarantees that at least one person is a survivor, for if each of these 2k + 1 people was hit by at least one pie, a total of at least 2k + 1 pies would have to be thr ...
... and B, at least three pies are thrown at A and B, and at most (2k + 3) − 3 = 2k pies are thrown at the remaining 2k + 1 people. This guarantees that at least one person is a survivor, for if each of these 2k + 1 people was hit by at least one pie, a total of at least 2k + 1 pies would have to be thr ...
Fibonacci numbers
... female, are put in a field; rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits; rabbits never die and a mating pair always produces one new pair (one male, one female) every month from the second month on. The puzzle ...
... female, are put in a field; rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits; rabbits never die and a mating pair always produces one new pair (one male, one female) every month from the second month on. The puzzle ...
Full text
... He and later writers on this topic were mainly concerned with the way in which N(x) affected T\(x) and vice versa. It can be seen that taking the g.p. to be a subset of the natural primes also fits the definition, but this covers a very large block of the total work done in Number Theory. Thus, this ...
... He and later writers on this topic were mainly concerned with the way in which N(x) affected T\(x) and vice versa. It can be seen that taking the g.p. to be a subset of the natural primes also fits the definition, but this covers a very large block of the total work done in Number Theory. Thus, this ...
Make Maths Make Sense: Basic Script
... a way that applies unchanged to small numbers, large numbers, vulgar fractions, decimal fractions, negative numbers, algebra and much else. This avoids the multitude of rules generally taught in maths (count the noughts; move the point; find the common denominator; multiply tops and bottoms; change ...
... a way that applies unchanged to small numbers, large numbers, vulgar fractions, decimal fractions, negative numbers, algebra and much else. This avoids the multitude of rules generally taught in maths (count the noughts; move the point; find the common denominator; multiply tops and bottoms; change ...
Significant Figures
... common digit occurring furthest to the right in all components. Another way to state this rule is as follows: in addition and subtraction, the result is rounded off so that it has the same number of digits as the measurement having the fewest decimal places (counting from left to right). For example ...
... common digit occurring furthest to the right in all components. Another way to state this rule is as follows: in addition and subtraction, the result is rounded off so that it has the same number of digits as the measurement having the fewest decimal places (counting from left to right). For example ...
I CHAPTER 3 Counting
... t may seem peculiar that a college-level text has a chapter on counting. At its most basic level, counting is a process of pointing to each object in a collection and calling off “one, two, three,...” until the quantity of objects is determined. How complex could that be? Actually, counting can beco ...
... t may seem peculiar that a college-level text has a chapter on counting. At its most basic level, counting is a process of pointing to each object in a collection and calling off “one, two, three,...” until the quantity of objects is determined. How complex could that be? Actually, counting can beco ...
Recitation 2
... Example 2a • Compute the average of set of n=2^k numbers – Avg({x1 .. xn})=(x1 +.. +xn)/n • Notice that: – Avg({x1 .. xn})=[Avg({x1 .. Xn/2})+Avg({xn/2+1 .. xn})]/2 • Algorithm 1. If input set size is 1, return the input as its average 2. Divide set into 2 subsets of n/2 if n>1 3. Find an average o ...
... Example 2a • Compute the average of set of n=2^k numbers – Avg({x1 .. xn})=(x1 +.. +xn)/n • Notice that: – Avg({x1 .. xn})=[Avg({x1 .. Xn/2})+Avg({xn/2+1 .. xn})]/2 • Algorithm 1. If input set size is 1, return the input as its average 2. Divide set into 2 subsets of n/2 if n>1 3. Find an average o ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.