Tutorial 1 material
... Any number can be written as a decimal number between 1 and 10 (called the digit term) multiplied by a power of 10. For example 357 can be written as 3.57 x 102 (I know this is actually more writing but we will see why it is useful shortly) Similarly 357.6 can be written as 3.576 x 102. Note that a ...
... Any number can be written as a decimal number between 1 and 10 (called the digit term) multiplied by a power of 10. For example 357 can be written as 3.57 x 102 (I know this is actually more writing but we will see why it is useful shortly) Similarly 357.6 can be written as 3.576 x 102. Note that a ...
Lehigh 2006 (no calculators) 1. 1/(1/3
... 2. Dick is 6 years older than Jane. Six years ago he was twice as old as she was. How old is Jane now? 3. A bicyclist riding against the wind averages 10 mph from A to B, but with the wind averages 15 mph returning from B to A . What is his average speed for the trip? 4. What is the largest possible ...
... 2. Dick is 6 years older than Jane. Six years ago he was twice as old as she was. How old is Jane now? 3. A bicyclist riding against the wind averages 10 mph from A to B, but with the wind averages 15 mph returning from B to A . What is his average speed for the trip? 4. What is the largest possible ...
selected solutions to Homework 11
... / S. Thus, S is not closed under addition and is not a subring. (b) This statement is true. Proof. Let R be a ring with unity, 1. Let a, b ∈ S. This means that there exist c, d ∈ R such that ac = 1 and bd = 1. Then (ab)(dc) = a(bd)c = a(1)(c) = (ac) = 1 Thus, (ab) ∈ S and S is closed under multiplic ...
... / S. Thus, S is not closed under addition and is not a subring. (b) This statement is true. Proof. Let R be a ring with unity, 1. Let a, b ∈ S. This means that there exist c, d ∈ R such that ac = 1 and bd = 1. Then (ab)(dc) = a(bd)c = a(1)(c) = (ac) = 1 Thus, (ab) ∈ S and S is closed under multiplic ...
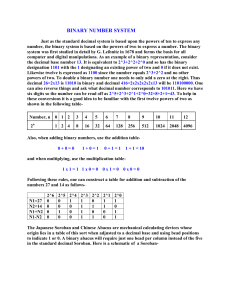
Representation of real numbers and integers
... Representation of real numbers and integers Representing a number in a computer Representing (or encoding) a number means to express it in binary form. Representing numbers in a computer is necessary in order for it to be able to store and manipulate them. However, the problem is that a mathematical ...
... Representation of real numbers and integers Representing a number in a computer Representing (or encoding) a number means to express it in binary form. Representing numbers in a computer is necessary in order for it to be able to store and manipulate them. However, the problem is that a mathematical ...
Times Tables Leaflet - Willow Tree Community Primary School
... Nine sixes? How many sixes in 42? Six times four? Forty-eight divided by six? Three multiplied by six? Six times what equals sixty Help them to use the table facts they remember easily to get to those which are harder: You can always say it the other way round - three eights are 24, so are eight thr ...
... Nine sixes? How many sixes in 42? Six times four? Forty-eight divided by six? Three multiplied by six? Six times what equals sixty Help them to use the table facts they remember easily to get to those which are harder: You can always say it the other way round - three eights are 24, so are eight thr ...
sample.problems - The Math Forum @ Drexel
... 4) Based on your results, what can you determine regarding the mean median and mode for the distributions above? 5) If the distribution continues proportionally as above, what is the frequency distribution for n=180 observations? 6) A probability mass function (PMF) expresses the frequency of each o ...
... 4) Based on your results, what can you determine regarding the mean median and mode for the distributions above? 5) If the distribution continues proportionally as above, what is the frequency distribution for n=180 observations? 6) A probability mass function (PMF) expresses the frequency of each o ...
Problem_Set_02
... a. The complement of the union of two sets equals the intersection of the complements. b. The complement of the intersection of two sets equals the union of the complements. c. (B A) (C A) = (B C) – A. d. If two sets are subsets of each other then they are equal. 2. Generalize De Morgan’s law ...
... a. The complement of the union of two sets equals the intersection of the complements. b. The complement of the intersection of two sets equals the union of the complements. c. (B A) (C A) = (B C) – A. d. If two sets are subsets of each other then they are equal. 2. Generalize De Morgan’s law ...
允許學生個人、非營利性的圖書館或公立學校合理使用 本
... 20. In this diagram there are four lines with three circles each. Place the numbers from 1 to 7 into the circles, so that each line adds up to 12. Which number must go into the circle at the centre of the diagram? (A) 7 (B) 6 (C) 5 (D) 4 (E) 2 Questions 21 to 25, 5 marks each 21. Four hockey teams p ...
... 20. In this diagram there are four lines with three circles each. Place the numbers from 1 to 7 into the circles, so that each line adds up to 12. Which number must go into the circle at the centre of the diagram? (A) 7 (B) 6 (C) 5 (D) 4 (E) 2 Questions 21 to 25, 5 marks each 21. Four hockey teams p ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.