Theorem 4.2: W6n+k - The Fibonacci Quarterly
... Some of the results in this paper are not as "practical" as others. For example, if we put n = 10 and k = 0 in (2.13), then we seek to find W40. However, on the right-hand side, we need to know W6, Wl2, Wls,..., W60 (and many other terms) in order to find W4Q. In contrast, (2.14) is more practical s ...
... Some of the results in this paper are not as "practical" as others. For example, if we put n = 10 and k = 0 in (2.13), then we seek to find W40. However, on the right-hand side, we need to know W6, Wl2, Wls,..., W60 (and many other terms) in order to find W4Q. In contrast, (2.14) is more practical s ...
Full text
... and this is clearly a number in the. sequence s. We must show that, for any difference A = | -pkl + Qkla | less than Ah9 the number sn - A is not in s. (By Lemma 2, the only-differences A that need be considered are, in fact, of the form | -pkl + qkia |.) Case 1: Even k. Here A = ~Pki+^kia • ^Y Lemm ...
... and this is clearly a number in the. sequence s. We must show that, for any difference A = | -pkl + Qkla | less than Ah9 the number sn - A is not in s. (By Lemma 2, the only-differences A that need be considered are, in fact, of the form | -pkl + qkia |.) Case 1: Even k. Here A = ~Pki+^kia • ^Y Lemm ...
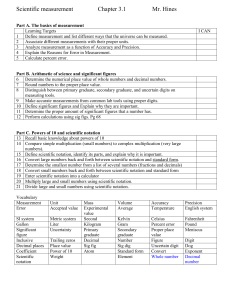
Scientific measurement - Campbell County Schools
... 6) If a decimal is not shown, it is always to the right of the number furthest to the right. B. What happens when a number is multiplied by a power of 10 1) 51 x 10 = 2) 368 x 10 = 3) 1 x 10 = 4) 900,000 x 10 = 5)347,922,222 x 10 = 6.) These are the same numbers listed– now where is the decimal C. W ...
... 6) If a decimal is not shown, it is always to the right of the number furthest to the right. B. What happens when a number is multiplied by a power of 10 1) 51 x 10 = 2) 368 x 10 = 3) 1 x 10 = 4) 900,000 x 10 = 5)347,922,222 x 10 = 6.) These are the same numbers listed– now where is the decimal C. W ...
2008 Questions
... 3. The Jones family averaged 90 km/h when they drove from Edmonton to their lake cottage. On the return trip, their average speed was only 75 km/h. Their average speed for the round trip, rounded to tenths, is A. 81.8 km/h B. 82.5 km/h C. impossible to determine because the distance from Edmonton to ...
... 3. The Jones family averaged 90 km/h when they drove from Edmonton to their lake cottage. On the return trip, their average speed was only 75 km/h. Their average speed for the round trip, rounded to tenths, is A. 81.8 km/h B. 82.5 km/h C. impossible to determine because the distance from Edmonton to ...
Inductive and Deductive Reasoning
... of numbers the y values and the order of the sequence the x 1st term is 2 2nd term is 4 3rd term is 6 4th term is 8 Pattern is they go up by 2 Next numbers in sequence are 10,12,14 ...
... of numbers the y values and the order of the sequence the x 1st term is 2 2nd term is 4 3rd term is 6 4th term is 8 Pattern is they go up by 2 Next numbers in sequence are 10,12,14 ...
Solutions to selected homework problems
... written as a sum of distinct primes (more than one prime). Solution: By Bertrand’s principle, for any k, there is a prime p with k < p < 2k. It follows that for any x (odd or even) there is a prime p with [x/2] < p < x. We prove the statement by (strong) induction. First 7 = 2+5. Now suppose every i ...
... written as a sum of distinct primes (more than one prime). Solution: By Bertrand’s principle, for any k, there is a prime p with k < p < 2k. It follows that for any x (odd or even) there is a prime p with [x/2] < p < x. We prove the statement by (strong) induction. First 7 = 2+5. Now suppose every i ...
Banff 2015
... It is not obvious that integer sequences - beyond those already in the curriculum deserve pedagogic attention. It is easy to imagine their uninspired use in the classroom… for example: all students asked to independently reproduce a meaningless sequence term by term. We won’t let that happen. Our st ...
... It is not obvious that integer sequences - beyond those already in the curriculum deserve pedagogic attention. It is easy to imagine their uninspired use in the classroom… for example: all students asked to independently reproduce a meaningless sequence term by term. We won’t let that happen. Our st ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.