Chapter 11 – Rational Functions
... Division by zero is an operation for which you cannot find an answer, so it is disallowed. You can understand why if you think about how division and multiplication are related. 12 divided by 6 is 2 because 6 times 2 is 12 12 divided by 0 is x would mean that 0 times x = 12 But no value would work f ...
... Division by zero is an operation for which you cannot find an answer, so it is disallowed. You can understand why if you think about how division and multiplication are related. 12 divided by 6 is 2 because 6 times 2 is 12 12 divided by 0 is x would mean that 0 times x = 12 But no value would work f ...
Answers to some typical exercises
... remainder 0 when divided by 6, then we have done. If none of them have remainder 0, then there are at most 5 cases (pigeonhole) of the remainder. Thus, at least two of them must have the same remainder. The positive difference of these two is a subsequence whose sum is divisible by 6. ...
... remainder 0 when divided by 6, then we have done. If none of them have remainder 0, then there are at most 5 cases (pigeonhole) of the remainder. Thus, at least two of them must have the same remainder. The positive difference of these two is a subsequence whose sum is divisible by 6. ...
File - Ms Dudek`s Website
... Three pigs entered a race around a track. Piggly takes 6 minutes to run one lap. Piglet takes 3 minutes to run one lap and it takes Wiggly 5 minutes to run one lap. If all three pigs begin the race at the same time, how many minutes will it take for all three pigs to be at the starting point again? ...
... Three pigs entered a race around a track. Piggly takes 6 minutes to run one lap. Piglet takes 3 minutes to run one lap and it takes Wiggly 5 minutes to run one lap. If all three pigs begin the race at the same time, how many minutes will it take for all three pigs to be at the starting point again? ...
Discrete Mathematics in the High School Curriculum.
... remove any one square the resulting squares can be covered by L-shaped trominos. For n = 1 this is obvious. Look at the next case, n = 2. Divide the original array into four quarters. The removed square came from one of these quarters. This quarter can be covered. If you can solve the problem of cov ...
... remove any one square the resulting squares can be covered by L-shaped trominos. For n = 1 this is obvious. Look at the next case, n = 2. Divide the original array into four quarters. The removed square came from one of these quarters. This quarter can be covered. If you can solve the problem of cov ...
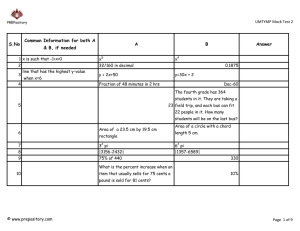
UMTYMP Mock Test 2
... Leslie, Ava, Eva and Daisy occupy four chairs in a square dining table. Leslie and Ava want to sit directly facing ...
... Leslie, Ava, Eva and Daisy occupy four chairs in a square dining table. Leslie and Ava want to sit directly facing ...
document
... Understand addition and subtraction of fractions; use the laws of arithmetic and inverse operations. Recall known facts, including fraction to decimal conversions; use known facts to derive unknown facts, including products such as 0.7 and 6, and 0.03 and 8. ...
... Understand addition and subtraction of fractions; use the laws of arithmetic and inverse operations. Recall known facts, including fraction to decimal conversions; use known facts to derive unknown facts, including products such as 0.7 and 6, and 0.03 and 8. ...
A 1 ∪A 2 ∪…∪A n |=|A 1 |+|A 2 |+…+|A n
... Theorem 4.6: The number of circular rpermutations of a set of n elements is given by p(n,r)/r=n!/r(n-r)! . In particular,the number of circular permutations of n elements is (n-1)! . Proof: The set of linear r-permutations can be partitioned into parts in such a way that two linear r-permutations ar ...
... Theorem 4.6: The number of circular rpermutations of a set of n elements is given by p(n,r)/r=n!/r(n-r)! . In particular,the number of circular permutations of n elements is (n-1)! . Proof: The set of linear r-permutations can be partitioned into parts in such a way that two linear r-permutations ar ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.