Algebra 1 Seamless Curriculum Guide
... 6.1 The student will understand the language and notation of function. Indicators: o Definition of relation o Definition of function o Domain, x value, input o Range, y value, output o Evaluate a function given a rule and a replacement set Vocabulary: relation, function, domain, range, f(x), input, ...
... 6.1 The student will understand the language and notation of function. Indicators: o Definition of relation o Definition of function o Domain, x value, input o Range, y value, output o Evaluate a function given a rule and a replacement set Vocabulary: relation, function, domain, range, f(x), input, ...
Decimal Notes Math SOL 4
... “A decimal point separates the whole number from the places that are less than one. Place values extend infinitely in two directions from a decimal point. A number containing a decimal point is called a decimal number or simply a decimal.” If, the whole illustration below equals one. How muc ...
... “A decimal point separates the whole number from the places that are less than one. Place values extend infinitely in two directions from a decimal point. A number containing a decimal point is called a decimal number or simply a decimal.” If, the whole illustration below equals one. How muc ...
Chapter 2 Study Guide
... 5. Check the units after doing the math. If the units are not what you were looking for, there is a mistake, however, correct units do not always mean you did the problem correctly. The answer to a dimensional analysis problem showing the correct number of sig. fig.’s, should equal the number of sig ...
... 5. Check the units after doing the math. If the units are not what you were looking for, there is a mistake, however, correct units do not always mean you did the problem correctly. The answer to a dimensional analysis problem showing the correct number of sig. fig.’s, should equal the number of sig ...
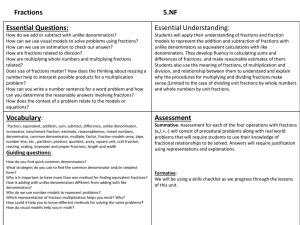
5 NF Unit Plan grade 5
... models to represent the addition and subtraction of fractions with unlike denominators as equivalent calculations with like denominators. They develop fluency in calculating sums and differences of fractions, and make reasonable estimates of them. Students also use the meaning of fractions, of multi ...
... models to represent the addition and subtraction of fractions with unlike denominators as equivalent calculations with like denominators. They develop fluency in calculating sums and differences of fractions, and make reasonable estimates of them. Students also use the meaning of fractions, of multi ...
Lecture-4
... 1. How would you use linspace to set up spacings for planting seedlets in a garden row (30 seedlets, each row 2 meters long). 2. How about planning a 4285km road trip on 21 days. How long each leg would be? ...
... 1. How would you use linspace to set up spacings for planting seedlets in a garden row (30 seedlets, each row 2 meters long). 2. How about planning a 4285km road trip on 21 days. How long each leg would be? ...
Section 2.3 - GEOCITIES.ws
... Example 3: Let’s translate the following verbal expression into an algebraic variable expression. the product of t and the sum of t and 12 STEP 1. the product of ( t and the sum of t and 12 ) Operation: Multiplication STEP 2. the product of ( t and the sum of t and 12 ) Note that inside the parenthe ...
... Example 3: Let’s translate the following verbal expression into an algebraic variable expression. the product of t and the sum of t and 12 STEP 1. the product of ( t and the sum of t and 12 ) Operation: Multiplication STEP 2. the product of ( t and the sum of t and 12 ) Note that inside the parenthe ...
PRIMITIVE SUBSTITUTIVE NUMBERS ARE CLOSED UNDER
... PRELIMINARIES This chapter consists of the notation and definitions of some of the concepts used throughout as well as some preliminary results about them which are not proved in this manuscript. It is by no means an exhaustive presentation of the relevant mathematical topics, but is simply intended ...
... PRELIMINARIES This chapter consists of the notation and definitions of some of the concepts used throughout as well as some preliminary results about them which are not proved in this manuscript. It is by no means an exhaustive presentation of the relevant mathematical topics, but is simply intended ...
Section 1.1
... Ex. 5: Examining an Unproven Conjecture Conjecture: Every even number greater than 2 can be written as the sum of two primes. This is called Goldbach’s Conjecture. No one has ever proven this conjecture is true or found a counterexample to show that it is false. As of the writing of this text, it i ...
... Ex. 5: Examining an Unproven Conjecture Conjecture: Every even number greater than 2 can be written as the sum of two primes. This is called Goldbach’s Conjecture. No one has ever proven this conjecture is true or found a counterexample to show that it is false. As of the writing of this text, it i ...
Rational Numbers Vocabulary Long
... Joe wants to have a party for his friends. He needs to buy two different sizes of plates; one for dinner, and one for dessert. The dinner plates come in packages of 10 and the dessert plates come in packages of 8. What is the smallest number of packages of each type of plate Joe needs to buy so he h ...
... Joe wants to have a party for his friends. He needs to buy two different sizes of plates; one for dinner, and one for dessert. The dinner plates come in packages of 10 and the dessert plates come in packages of 8. What is the smallest number of packages of each type of plate Joe needs to buy so he h ...
Accuracy and Precision SIGNIFICANT FIGURES
... Significant Figures in Numerical Calculations 1) Multiplication or Division The result of multiplication or division, may contain only as many sig. fig. as the least precisely known quantity in the calculation. E.g. 14.79cm x 12.11cm x 5.05cm = 904cm (4 sig.fig) (4 sig. fig) (3 sig. fig) (3 sig fig ...
... Significant Figures in Numerical Calculations 1) Multiplication or Division The result of multiplication or division, may contain only as many sig. fig. as the least precisely known quantity in the calculation. E.g. 14.79cm x 12.11cm x 5.05cm = 904cm (4 sig.fig) (4 sig. fig) (3 sig. fig) (3 sig fig ...
Addition
Addition (often signified by the plus symbol ""+"") is one of the four elementary, mathematical operations of arithmetic, with the others being subtraction, multiplication and division.The addition of two whole numbers is the total amount of those quantities combined. For example, in the picture on the right, there is a combination of three apples and two apples together; making a total of 5 apples. This observation is equivalent to the mathematical expression ""3 + 2 = 5"" i.e., ""3 add 2 is equal to 5"".Besides counting fruits, addition can also represent combining other physical objects. Using systematic generalizations, addition can also be defined on more abstract quantities, such as integers, rational numbers, real numbers and complex numbers and other abstract objects such as vectors and matrices.In arithmetic, rules for addition involving fractions and negative numbers have been devised amongst others. In algebra, addition is studied more abstractly.Addition has several important properties. It is commutative, meaning that order does not matter, and it is associative, meaning that when one adds more than two numbers, the order in which addition is performed does not matter (see Summation). Repeated addition of 1 is the same as counting; addition of 0 does not change a number. Addition also obeys predictable rules concerning related operations such as subtraction and multiplication.Performing addition is one of the simplest numerical tasks. Addition of very small numbers is accessible to toddlers; the most basic task, 1 + 1, can be performed by infants as young as five months and even some non-human animals. In primary education, students are taught to add numbers in the decimal system, starting with single digits and progressively tackling more difficult problems. Mechanical aids range from the ancient abacus to the modern computer, where research on the most efficient implementations of addition continues to this day.