C++ for beginners lecture 1
... C++ is type sensitive value = identifier C++ is case sensitive 12 = initial value of 'value' should be a whole number (as it is stored into an int) ...
... C++ is type sensitive value = identifier C++ is case sensitive 12 = initial value of 'value' should be a whole number (as it is stored into an int) ...
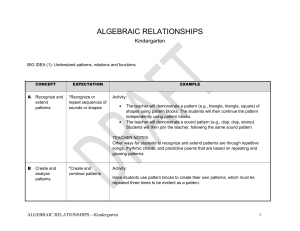
Algebraic Relationships
... red” is the same in form as “clap, clap, step, clap, clap, step, clap, clap, step.” This recognition lays the foundation for the idea that two very different situations can have the same mathematical features and are the same in some important ways. Knowing that each pattern could be described as ha ...
... red” is the same in form as “clap, clap, step, clap, clap, step, clap, clap, step.” This recognition lays the foundation for the idea that two very different situations can have the same mathematical features and are the same in some important ways. Knowing that each pattern could be described as ha ...
Next-Generation Arithmetic Sample Questions - Accuplacer
... of 3.9 by 2.84 results in 2.556 and then multiplying the ones place of 3.9 by 2.84 results in 8.520, since each product must have three places to the right of the decimal. The sum of these two numbers is 2.556 + 8.520 = 11.076. Choice A is incorrect. This results from not using a placeholder zero wh ...
... of 3.9 by 2.84 results in 2.556 and then multiplying the ones place of 3.9 by 2.84 results in 8.520, since each product must have three places to the right of the decimal. The sum of these two numbers is 2.556 + 8.520 = 11.076. Choice A is incorrect. This results from not using a placeholder zero wh ...
Introduction to the Theory of Computation
... His proof: if it were raining (assuming the statement Proof: here Jill are the n be consecutive composite integers is false), woud wet (contradiction, or false for any n: consequence). Therefore, it must not be raining. (n+1)!+2, (n+1)!+3, ..., (n+1)!+n+1 ...
... His proof: if it were raining (assuming the statement Proof: here Jill are the n be consecutive composite integers is false), woud wet (contradiction, or false for any n: consequence). Therefore, it must not be raining. (n+1)!+2, (n+1)!+3, ..., (n+1)!+n+1 ...
Full text
... system, where 5 is equivalent to both F5 and F4 + F3. It is known (e.g., Brown [1]) that an wtuple of 0's and l's is a unique representative of N if every pair of lfs is separated by at least one 0. Under this restriction, we view 1000 as the representative of 5 and 0110 as the redundant representat ...
... system, where 5 is equivalent to both F5 and F4 + F3. It is known (e.g., Brown [1]) that an wtuple of 0's and l's is a unique representative of N if every pair of lfs is separated by at least one 0. Under this restriction, we view 1000 as the representative of 5 and 0110 as the redundant representat ...
Elementary mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. The most basic topics in elementary mathematics are arithmetic and geometry. Beginning in the last decades of the 20th century, there has been an increased emphasis on problem solving. Elementary mathematics is used in everyday life in such activities as making change, cooking, buying and selling stock, and gambling. It is also an essential first step on the path to understanding science.In secondary school, the main topics in elementary mathematics are algebra and trigonometry. Calculus, even though it is often taught to advanced secondary school students, is usually considered college level mathematics.