ppt
... First the prompt is printed The input function waits for the user to enter a value and press
The expression that was entered is
evaluated to turn it from a string of
characters into a Python value (say, a
number).
The value is assigned to the variable.
Python Programming, 2/e
...
... First the prompt is printed The input function waits for the user to enter a value and press
pptx
... Digital computers are implemented via logic circuits and thus represent all numbers in binary (base 2) We (humans) often write numbers as decimal and hexadecimal for convenience, so need to be able to convert to binary and back (to understand what computer is doing!) Adding two 1-bit numbers genera ...
... Digital computers are implemented via logic circuits and thus represent all numbers in binary (base 2) We (humans) often write numbers as decimal and hexadecimal for convenience, so need to be able to convert to binary and back (to understand what computer is doing!) Adding two 1-bit numbers genera ...
MM2009 Maths Methods 2
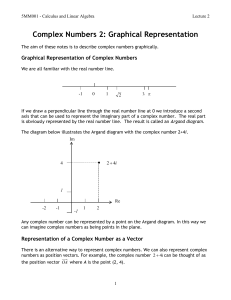
... If z x yi then the point P(x, y) can be represented by the polar co-ordinate r , where r is called the modulus and is the length OP and θ, the argument, is the angle made by OP with the real axis. Calculating the Modulus The modulus, written z is calculated via Pythagoras’ formula ...
... If z x yi then the point P(x, y) can be represented by the polar co-ordinate r , where r is called the modulus and is the length OP and θ, the argument, is the angle made by OP with the real axis. Calculating the Modulus The modulus, written z is calculated via Pythagoras’ formula ...
Double precision floating point
... none in quality and performance. Thousands of Intel employees work very hard to ensure that this is true. But no microprocessor is ever perfect. What Intel continues to believe is technically an extremely minor problem has taken on a life of its own. Although Intel firmly stands behind the quality o ...
... none in quality and performance. Thousands of Intel employees work very hard to ensure that this is true. But no microprocessor is ever perfect. What Intel continues to believe is technically an extremely minor problem has taken on a life of its own. Although Intel firmly stands behind the quality o ...
Lecture Notes - jan.ucc.nau.edu
... Proof by Contradiction: Example • Theorem: There exists an infinite number of prime numbers. • Proof (courtesy of Euclid): 1. Assume that there are a finite number of primes. 2. Then there is a largest prime, p. Consider the number q = (2x3x5x7x...xp)+1. q is one more than the product of all primes ...
... Proof by Contradiction: Example • Theorem: There exists an infinite number of prime numbers. • Proof (courtesy of Euclid): 1. Assume that there are a finite number of primes. 2. Then there is a largest prime, p. Consider the number q = (2x3x5x7x...xp)+1. q is one more than the product of all primes ...
Elementary mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. The most basic topics in elementary mathematics are arithmetic and geometry. Beginning in the last decades of the 20th century, there has been an increased emphasis on problem solving. Elementary mathematics is used in everyday life in such activities as making change, cooking, buying and selling stock, and gambling. It is also an essential first step on the path to understanding science.In secondary school, the main topics in elementary mathematics are algebra and trigonometry. Calculus, even though it is often taught to advanced secondary school students, is usually considered college level mathematics.