Sixth - Bergen.org
... 23. How many multiples of 17 are three-digit positive integers? 24. Young Guy is selecting toppings for ice cream. There are 3 options: sprinkles, whipped cream, and fudge. If he is allowed to select any number of toppings, or no toppings at all, how many different ways can he have ice cream? 25. A ...
... 23. How many multiples of 17 are three-digit positive integers? 24. Young Guy is selecting toppings for ice cream. There are 3 options: sprinkles, whipped cream, and fudge. If he is allowed to select any number of toppings, or no toppings at all, how many different ways can he have ice cream? 25. A ...
Math for Poets and Drummers
... consider the following puzzle: How many different meters are there of a given duration? The solution to this problem is suggested by figure 1, in which 1 × 1 squares and 1 × 2 rectangles represent short and long syllables, respectively. The numbers of patterns of each duration form the sequence 1, 2 ...
... consider the following puzzle: How many different meters are there of a given duration? The solution to this problem is suggested by figure 1, in which 1 × 1 squares and 1 × 2 rectangles represent short and long syllables, respectively. The numbers of patterns of each duration form the sequence 1, 2 ...
4 – 6 Arithmetic Sequences WW: sequence, term, arithmetic
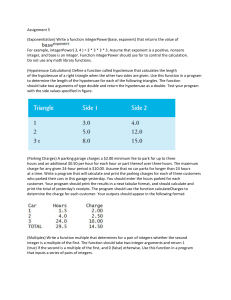
... EQ: How is identifying an arithmetic sequence similar to identifying a function rule? When you list the times and distances in order, each list forms a sequence. A sequence is a list of numbers that often forms a pattern. Each number in a sequence is a term. When the terms of a sequence differ by th ...
... EQ: How is identifying an arithmetic sequence similar to identifying a function rule? When you list the times and distances in order, each list forms a sequence. A sequence is a list of numbers that often forms a pattern. Each number in a sequence is a term. When the terms of a sequence differ by th ...
Collatz conjecture

The Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse), or the Syracuse problem; the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers (because the values are usually subject to multiple descents and ascents like hailstones in a cloud), or as wondrous numbers.Take any natural number n. If n is even, divide it by 2 to get n / 2. If n is odd, multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process (which has been called ""Half Or Triple Plus One"", or HOTPO) indefinitely. The conjecture is that no matter what number you start with, you will always eventually reach 1. The property has also been called oneness.Paul Erdős said about the Collatz conjecture: ""Mathematics may not be ready for such problems."" He also offered $500 for its solution.