9-1
... Carlo uses a double-pan balance and three different weights to weigh bird seed. If his weights are 1 lb, 2 lb, and 5 lb, what whole pound amounts is he able to weigh? 1, 2, 3, 5, 6, 7, and 8 lb ...
... Carlo uses a double-pan balance and three different weights to weigh bird seed. If his weights are 1 lb, 2 lb, and 5 lb, what whole pound amounts is he able to weigh? 1, 2, 3, 5, 6, 7, and 8 lb ...
Unit 1C - Rational Numbers
... Common Core Standard: 6.NS.C.8 Solve real-world and mathematical problem by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate. Learning Target: I c ...
... Common Core Standard: 6.NS.C.8 Solve real-world and mathematical problem by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate. Learning Target: I c ...
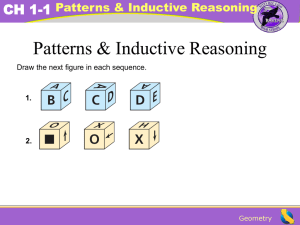
ch 5 finding a pattern notes
... to work for the inputs 2 and 4. Experimenting further shows you that this rule works for all the inputs. Now that we know that x+5 is the function rule to apply to each input, determining the output for an input of 895 is easy: 895+5=900. ...
... to work for the inputs 2 and 4. Experimenting further shows you that this rule works for all the inputs. Now that we know that x+5 is the function rule to apply to each input, determining the output for an input of 895 is easy: 895+5=900. ...
Full text
... For larger values of m9 it is convenient to use recursion formulas with positive terms only 9 which will be connected with a closer investigation of irregular permutations. If we start from one of the um permutations belonging to U(m9 0)s say a9 and if we delete 7??+ 1 in a, the remaining permutatio ...
... For larger values of m9 it is convenient to use recursion formulas with positive terms only 9 which will be connected with a closer investigation of irregular permutations. If we start from one of the um permutations belonging to U(m9 0)s say a9 and if we delete 7??+ 1 in a, the remaining permutatio ...
Collatz conjecture

The Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture (after Stanisław Ulam), Kakutani's problem (after Shizuo Kakutani), the Thwaites conjecture (after Sir Bryan Thwaites), Hasse's algorithm (after Helmut Hasse), or the Syracuse problem; the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers (because the values are usually subject to multiple descents and ascents like hailstones in a cloud), or as wondrous numbers.Take any natural number n. If n is even, divide it by 2 to get n / 2. If n is odd, multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process (which has been called ""Half Or Triple Plus One"", or HOTPO) indefinitely. The conjecture is that no matter what number you start with, you will always eventually reach 1. The property has also been called oneness.Paul Erdős said about the Collatz conjecture: ""Mathematics may not be ready for such problems."" He also offered $500 for its solution.