B - Computer Science
... Form a new real number with the decimal expansion where r is not equal to any of the r1 , r2 , r3 ,... Because it differs from ri in its ith position after the decimal point. Therefore there is a real number between 0 and 1 that is not on the list since every real number has a unique decimal expansi ...
... Form a new real number with the decimal expansion where r is not equal to any of the r1 , r2 , r3 ,... Because it differs from ri in its ith position after the decimal point. Therefore there is a real number between 0 and 1 that is not on the list since every real number has a unique decimal expansi ...
Algebra 2 - peacock
... A finite set has a definite, or finite, number of elements. An infinite set has an unlimited, or infinite number of elements. The Density Property states that between any two numbers there is another real number. So any interval that includes more than one point contains infinitely many points. ...
... A finite set has a definite, or finite, number of elements. An infinite set has an unlimited, or infinite number of elements. The Density Property states that between any two numbers there is another real number. So any interval that includes more than one point contains infinitely many points. ...
ppt - Purdue College of Engineering
... • A tautology is a formula that is true in every model. (also called a theorem) – for example, (A A) is a tautology – What about (AB)(AB)? – Look at tautological equivalences on pg. 8 of text ...
... • A tautology is a formula that is true in every model. (also called a theorem) – for example, (A A) is a tautology – What about (AB)(AB)? – Look at tautological equivalences on pg. 8 of text ...
Monotone Sequence and Limit theorem
... To bring this estimate to the required form, we make some changes. We choose and if ...
... To bring this estimate to the required form, we make some changes. We choose and if ...
Applications of imaginary numbers
... backwards" by taking the square root). Every number was positive after you squared it. So you couldn't very well square-root a negative and expect to come up with anything sensible. Now, however, you can take the square root of a negative number, but it involves using a new number to do it. This new ...
... backwards" by taking the square root). Every number was positive after you squared it. So you couldn't very well square-root a negative and expect to come up with anything sensible. Now, however, you can take the square root of a negative number, but it involves using a new number to do it. This new ...
13-3 Other Sequences
... By looking at the sequence 1, 2, 3, 4, 5, . . ., you would probably assume that the next term is 6. In fact, the next term could be any number. If no rule is given, you should use the simplest recognizable pattern in the given terms. ...
... By looking at the sequence 1, 2, 3, 4, 5, . . ., you would probably assume that the next term is 6. In fact, the next term could be any number. If no rule is given, you should use the simplest recognizable pattern in the given terms. ...
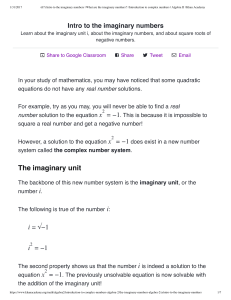
The imaginary unit
... Pure imaginary numbers The number i is by no means alone! By taking multiples of this imaginary unit, we can create infinitely many more pure imaginary numbers. For example, 3i, i√5, and −12i are all examples of pure imaginary numbers, or numbers of the form bi, where b is a nonzero real number. Taki ...
... Pure imaginary numbers The number i is by no means alone! By taking multiples of this imaginary unit, we can create infinitely many more pure imaginary numbers. For example, 3i, i√5, and −12i are all examples of pure imaginary numbers, or numbers of the form bi, where b is a nonzero real number. Taki ...