Finding Complex Solutions of Quadratic Equations
... , which gives the solutions of the general quadratic equation. In the quadratic formula, the formula, x = ___________ 2a expression under the radical sign, b 2 - 4ac, is called the discriminant, and its value determines whether the solutions of the quadratic equation are real or non-real. ...
... , which gives the solutions of the general quadratic equation. In the quadratic formula, the formula, x = ___________ 2a expression under the radical sign, b 2 - 4ac, is called the discriminant, and its value determines whether the solutions of the quadratic equation are real or non-real. ...
Document
... 1. Dirichet boundary condition: The physical quantities on the boundaries are specified. 2. Neumann boundary condition: The normal derivatives of the physical quantities on the boundaries are given. 3. Mixed boundary-value condition: The physical quantities on some boundaries are given, and the norm ...
... 1. Dirichet boundary condition: The physical quantities on the boundaries are specified. 2. Neumann boundary condition: The normal derivatives of the physical quantities on the boundaries are given. 3. Mixed boundary-value condition: The physical quantities on some boundaries are given, and the norm ...
thermodynamics type 1
... Chemical reactions are generally carried out at constant pressure (atmospheric pressure) so it has been found useful to define a new state function Enthalpy (H) as : H = E + PV (By definition) or ∆H = ∆E + P ∆V + V∆P or ∆H = ∆E + P ∆V (at constant pressure) combining with first law. Equation (1) bec ...
... Chemical reactions are generally carried out at constant pressure (atmospheric pressure) so it has been found useful to define a new state function Enthalpy (H) as : H = E + PV (By definition) or ∆H = ∆E + P ∆V + V∆P or ∆H = ∆E + P ∆V (at constant pressure) combining with first law. Equation (1) bec ...
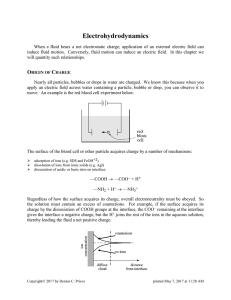
Electrohydrodynamics
... The argument of the sinh must be dimensionless, so let’s use this combination to define a new dimensionless potential ...
... The argument of the sinh must be dimensionless, so let’s use this combination to define a new dimensionless potential ...