Factoring Polynomials: The Greatest Common Factor
... essential skill for success in algebra and higher level mathematics courses. Therefore, we have taken great care in developing the student's understanding of the factorization process. The technique is consistently illustrated by displaying an empty set of parentheses and describing the thought proc ...
... essential skill for success in algebra and higher level mathematics courses. Therefore, we have taken great care in developing the student's understanding of the factorization process. The technique is consistently illustrated by displaying an empty set of parentheses and describing the thought proc ...
fraction basics - Lone Star College
... The LCM of two numbers is the smallest multiple that both of the numbers have in common. In other words, the LCM is the smallest number divisible evenly by both of the numbers. The LCM is the same as the LCD. Example: ...
... The LCM of two numbers is the smallest multiple that both of the numbers have in common. In other words, the LCM is the smallest number divisible evenly by both of the numbers. The LCM is the same as the LCD. Example: ...
Polynomials
... Standard: MM1A2c Add, subtract, multiply and divide polynomials. Today’s Question: What are polynomials, and how do we add, subtract and multiply them? Standard: MM1A2c. ...
... Standard: MM1A2c Add, subtract, multiply and divide polynomials. Today’s Question: What are polynomials, and how do we add, subtract and multiply them? Standard: MM1A2c. ...
I(x)
... IV054 Hamming codes as cyclic codes Definition (Again!) Let r be a positive integer and let H be an r * (2r -1) matrix whose columns are distinct non-zero vectors of V(r,2). Then the code having H as its parity-check matrix is called binary Hamming code denoted by Ham (r,2). It can be shown that bi ...
... IV054 Hamming codes as cyclic codes Definition (Again!) Let r be a positive integer and let H be an r * (2r -1) matrix whose columns are distinct non-zero vectors of V(r,2). Then the code having H as its parity-check matrix is called binary Hamming code denoted by Ham (r,2). It can be shown that bi ...
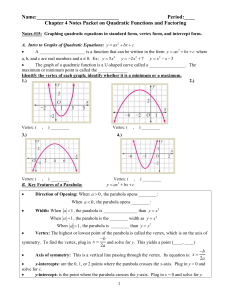
Day 57 - 61 EOC Quadratics Reivew
... 2nd: Factor out the GCF 3rd: Complete the X & box method to find the factors 4th: Set every factor that contains an x in it, equal to 0 & solve for x. B.) Completing the Square 1st: Move the constant (number with no variable) to the right so that all variables are on the left & all constants are on ...
... 2nd: Factor out the GCF 3rd: Complete the X & box method to find the factors 4th: Set every factor that contains an x in it, equal to 0 & solve for x. B.) Completing the Square 1st: Move the constant (number with no variable) to the right so that all variables are on the left & all constants are on ...
CHAPTER 3: Cyclic Codes
... IV054 Hamming codes as cyclic codes Definition (Again!) Let r be a positive integer and let H be an r * (2r -1) matrix whose columns are distinct non-zero vectors of V(r,2). Then the code having H as its parity-check matrix is called binary Hamming code denoted by Ham (r,2). It can be shown that bi ...
... IV054 Hamming codes as cyclic codes Definition (Again!) Let r be a positive integer and let H be an r * (2r -1) matrix whose columns are distinct non-zero vectors of V(r,2). Then the code having H as its parity-check matrix is called binary Hamming code denoted by Ham (r,2). It can be shown that bi ...
POLYNOMIALS WITH DIVISORS OF EVERY DEGREE 1
... Unfortunately, this criterion for ϕ-practicality is not particularly useful to us, since the totients of divisors of n are not monotonic in general. To get around these problems, we will only give a necessary condition for a number to be ϕ-practical, which is all that is needed in order to determine ...
... Unfortunately, this criterion for ϕ-practicality is not particularly useful to us, since the totients of divisors of n are not monotonic in general. To get around these problems, we will only give a necessary condition for a number to be ϕ-practical, which is all that is needed in order to determine ...
#3 - 1.2 Square Roots of Non
... We will continue working on the Math 9 Specific Curriculum Outcome (SCO) "Numbers 4" OR N4 and begin working on "Numbers 6" OR "N6" which state: N4: "Explain and apply the order of operations, including exponents, with and without technology." N6: "Determine an approximate square root of positiv ...
... We will continue working on the Math 9 Specific Curriculum Outcome (SCO) "Numbers 4" OR N4 and begin working on "Numbers 6" OR "N6" which state: N4: "Explain and apply the order of operations, including exponents, with and without technology." N6: "Determine an approximate square root of positiv ...
19(5)
... Articles should be submitted in the format of the current issues of the Quarterly. They should be typewritten or reproduced typewritten copies, double space with wide margins and on only one side of the paper. Articles should be no longer than twenty-five pages. The full name and address of the auth ...
... Articles should be submitted in the format of the current issues of the Quarterly. They should be typewritten or reproduced typewritten copies, double space with wide margins and on only one side of the paper. Articles should be no longer than twenty-five pages. The full name and address of the auth ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.
![[hal-00137158, v1] Well known theorems on triangular systems and](http://s1.studyres.com/store/data/015177460_1-823a690e284005713c70fc9e95ccaaf8-300x300.png)