Algebra Qualifying Exam January 2015
... (c) Let K a field which is NOT algebraically closed. Give an example of a maximal ideal of the ring R = K[X, Y ] which is NOT of the form (X − a, Y − b) with a, b ∈ K (recall that a field L is algebraically closed if every non-constant polynomial f (X) ∈ L[X] has at least a root in L; this problem i ...
... (c) Let K a field which is NOT algebraically closed. Give an example of a maximal ideal of the ring R = K[X, Y ] which is NOT of the form (X − a, Y − b) with a, b ∈ K (recall that a field L is algebraically closed if every non-constant polynomial f (X) ∈ L[X] has at least a root in L; this problem i ...
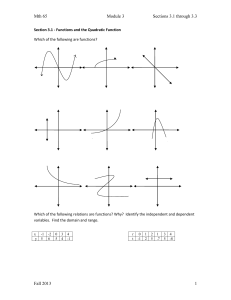
Mth 65 Module 3 Sections 3.1 through 3.3 Section 3.1
... not repeat. Irrational numbers cannot be written as ratios. (The square root of any non-perfect square number is irrational.) ...
... not repeat. Irrational numbers cannot be written as ratios. (The square root of any non-perfect square number is irrational.) ...
PDF
... The empty sum is such a borderline case of sum where the number of the addends is zero, i.e. the set of the addends is an empty set. • One may think that the zeroth multiple 0a of a ring element a is the empty sum; it can spring up by adding in the ring two multiples whose integer coefficients are o ...
... The empty sum is such a borderline case of sum where the number of the addends is zero, i.e. the set of the addends is an empty set. • One may think that the zeroth multiple 0a of a ring element a is the empty sum; it can spring up by adding in the ring two multiples whose integer coefficients are o ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.