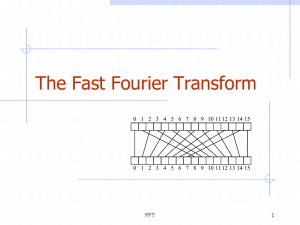
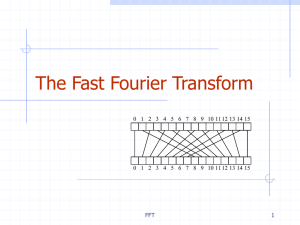
Prime Factorization
... Which method should we use? • Both division by primes and factor tree may be used in any case; however, one method may make the problem much easier. • Often it is best to use division by primes when it is difficult to see large numbers that can be used. • Factor tree is a good choice when it is eas ...
... Which method should we use? • Both division by primes and factor tree may be used in any case; however, one method may make the problem much easier. • Often it is best to use division by primes when it is difficult to see large numbers that can be used. • Factor tree is a good choice when it is eas ...
Factors of disconnected graphs and polynomials with nonnegative
... Proof. It is clear from the definition that the set Γ̃0 is just the free Abelian group generated by the connected graphs. If in a formal sum all weights aG are nonnegative, then the formal sum is just a graph as we know it. Conversely, every graph can be written as such a sum in exactly one way, bec ...
... Proof. It is clear from the definition that the set Γ̃0 is just the free Abelian group generated by the connected graphs. If in a formal sum all weights aG are nonnegative, then the formal sum is just a graph as we know it. Conversely, every graph can be written as such a sum in exactly one way, bec ...
IOSR Journal of Applied Physics (IOSR-JAP)
... of that of sun, is the most massive among other planets). The outer family have widely spaced orbits; Consists mainly gaseous material. The four planets in our inner planet category contain the first four planets including our mother earth. All these planets have radius less than one tenth of the Ju ...
... of that of sun, is the most massive among other planets). The outer family have widely spaced orbits; Consists mainly gaseous material. The four planets in our inner planet category contain the first four planets including our mother earth. All these planets have radius less than one tenth of the Ju ...
Subfield-Compatible Polynomials over Finite Fields - Rose
... any function on E. This paper presents conditions that characterize when the restriction of g to the subfield K maps entirely into L, i.e. g (K) ⊆ L. When this occurs, we say that g is K to L compatible. When we say that a polynomial f ∈ E[x] is K to L compatible, we mean that f (α) ∈ L for all α ∈ ...
... any function on E. This paper presents conditions that characterize when the restriction of g to the subfield K maps entirely into L, i.e. g (K) ⊆ L. When this occurs, we say that g is K to L compatible. When we say that a polynomial f ∈ E[x] is K to L compatible, we mean that f (α) ∈ L for all α ∈ ...
2009 USA Team Selection Test
... Let N > M > 1 be fixed integers. There are N people playing in a chess tournament; each pair of players plays each other once, with no draws. It turns out that for each sequence of M + 1 distinct players P0 , P1 , . . . PM such that Pi−1 beat Pi for each i = 1, . . . , M , player P0 also beat PM . P ...
... Let N > M > 1 be fixed integers. There are N people playing in a chess tournament; each pair of players plays each other once, with no draws. It turns out that for each sequence of M + 1 distinct players P0 , P1 , . . . PM such that Pi−1 beat Pi for each i = 1, . . . , M , player P0 also beat PM . P ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.