The Critical Thread:
... Mathematics is not a linear object. Though it may start off in such a fashion, soon it is a interweaving fabric of logic and definitions which create a coherent system of solving problems. Indeed, at the heart of Mathematics is logic. Once a definition in Mathematics is made, all the results that fo ...
... Mathematics is not a linear object. Though it may start off in such a fashion, soon it is a interweaving fabric of logic and definitions which create a coherent system of solving problems. Indeed, at the heart of Mathematics is logic. Once a definition in Mathematics is made, all the results that fo ...
15(1)
... / = 0, 1, 2, 3, 4 but composite for / = 5, 6. It is an unsolved problem whether or not 22' + 1 has other prime values. We note in passing that, when k = 2,F6=8 = 23, and 8m ± 1 = (23 ) ^ ± 1 = (2m ) 3 ± 7 is always composite, since A 3 ± B is always factorable. It is th ought that Fg + 1 is a prime. ...
... / = 0, 1, 2, 3, 4 but composite for / = 5, 6. It is an unsolved problem whether or not 22' + 1 has other prime values. We note in passing that, when k = 2,F6=8 = 23, and 8m ± 1 = (23 ) ^ ± 1 = (2m ) 3 ± 7 is always composite, since A 3 ± B is always factorable. It is th ought that Fg + 1 is a prime. ...
Algebra II Lesson Plans for Block Schedule
... problems; justify results. a) Solve using tables, graphs, and algebraic properties. “SAP”: Students will work in collaborative pairs to complete the Number Tile Puzzle. Lesson Anatomy: 1. Teacher led discussion of troublesome homework problems. 2. Quiz on solving equations and inequalities. 3. Solve ...
... problems; justify results. a) Solve using tables, graphs, and algebraic properties. “SAP”: Students will work in collaborative pairs to complete the Number Tile Puzzle. Lesson Anatomy: 1. Teacher led discussion of troublesome homework problems. 2. Quiz on solving equations and inequalities. 3. Solve ...
SD 9-12 Algebra
... Variation equations are formulas that show how one quantity changes in relation to one or more other quantities. There are four types of variation: direct, indirect (or inverse), joint, and combined. Direct variation equations show a relationship between two quantities such that when one quantity in ...
... Variation equations are formulas that show how one quantity changes in relation to one or more other quantities. There are four types of variation: direct, indirect (or inverse), joint, and combined. Direct variation equations show a relationship between two quantities such that when one quantity in ...
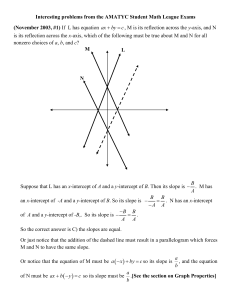
Interesting problems from the AMATYC Student Math League Exams
... So the correct answer is D) 96. [See the section on Logarithmic Properties] (February 2004, #7) The number 877530p765q6 is divisible by both 8 and 11, with p and q both digits from 0 to 9. The number is also divisible by In order for the number to be divisible by 8, 5q6, the number consisting of the ...
... So the correct answer is D) 96. [See the section on Logarithmic Properties] (February 2004, #7) The number 877530p765q6 is divisible by both 8 and 11, with p and q both digits from 0 to 9. The number is also divisible by In order for the number to be divisible by 8, 5q6, the number consisting of the ...
Advanced NUMBERTHEORY
... The present text constitutes slightly more than enough for a secondsemester course, carrying the student on to the twentieth Century by motivating some heroic nineteenth-Century developments in algebra and analysis. The relation of this textbook to the great treatises Will necessarily be like that o ...
... The present text constitutes slightly more than enough for a secondsemester course, carrying the student on to the twentieth Century by motivating some heroic nineteenth-Century developments in algebra and analysis. The relation of this textbook to the great treatises Will necessarily be like that o ...
Math 6+: Algebra
... * At the range mid-point, this is the probability students would correctly answer items measuring these concepts and skills. Both data from test items and review by NWEA curriculum specialists are used to place Learning Continuum statements into appropriate RIT ranges. Blank cells indicate data are ...
... * At the range mid-point, this is the probability students would correctly answer items measuring these concepts and skills. Both data from test items and review by NWEA curriculum specialists are used to place Learning Continuum statements into appropriate RIT ranges. Blank cells indicate data are ...
Full text
... which to date has not been determined in a precise manner. In the face of this situations what remains to be done? The present a r t i cle attacks this problem by attempting to accomplish two things.9 (1) Determining the relations among cognate formulas so that formulas can be grouped into families ...
... which to date has not been determined in a precise manner. In the face of this situations what remains to be done? The present a r t i cle attacks this problem by attempting to accomplish two things.9 (1) Determining the relations among cognate formulas so that formulas can be grouped into families ...
Kendriya Vidyalya Sangathan New Delhi
... Q4. How many solutions of the equation 5x-4y+11=0 are possible? Q5. What is the value of ‘K’ for which the graph of the equations 2x-3y=9 and kx-9y=18 are parallel lines? Q6. Find the value of ‘a’ for which the system of equations 3x+2y-4=0 and ax-y-3=0 will represent intersecting lines? Q. Write a ...
... Q4. How many solutions of the equation 5x-4y+11=0 are possible? Q5. What is the value of ‘K’ for which the graph of the equations 2x-3y=9 and kx-9y=18 are parallel lines? Q6. Find the value of ‘a’ for which the system of equations 3x+2y-4=0 and ax-y-3=0 will represent intersecting lines? Q. Write a ...
a(x)
... • Theorem true if n is prime, because ø(n) =(n‐1) & fermat’s thm holds. • Consider the set of integers, as R={x1,x2,..x ø(n)} • That is each element xi of R is a unique positive integer less than n with gcd(x i,n)=1 • Now multiply with a, modulo n • S={(ax1 mod n), (ax2 mod n).....(a x ø(n) mod n ...
... • Theorem true if n is prime, because ø(n) =(n‐1) & fermat’s thm holds. • Consider the set of integers, as R={x1,x2,..x ø(n)} • That is each element xi of R is a unique positive integer less than n with gcd(x i,n)=1 • Now multiply with a, modulo n • S={(ax1 mod n), (ax2 mod n).....(a x ø(n) mod n ...
Lesson 1
... As mentioned, we can use variables and algebraic expressions to describe certain quantitative relationships without information about their specific values. In a certain store, a cake costs 5 dollars. Let x be a variable that represents the number of cakes we plan to buy in that store. To calculate ...
... As mentioned, we can use variables and algebraic expressions to describe certain quantitative relationships without information about their specific values. In a certain store, a cake costs 5 dollars. Let x be a variable that represents the number of cakes we plan to buy in that store. To calculate ...
Factorization
In mathematics, factorization (also factorisation in some forms of British English) or factoring is the decomposition of an object (for example, a number, a polynomial, or a matrix) into a product of other objects, or factors, which when multiplied together give the original. For example, the number 15 factors into primes as 3 × 5, and the polynomial x2 − 4 factors as (x − 2)(x + 2). In all cases, a product of simpler objects is obtained.The aim of factoring is usually to reduce something to “basic building blocks”, such as numbers to prime numbers, or polynomials to irreducible polynomials. Factoring integers is covered by the fundamental theorem of arithmetic and factoring polynomials by the fundamental theorem of algebra. Viète's formulas relate the coefficients of a polynomial to its roots.The opposite of polynomial factorization is expansion, the multiplying together of polynomial factors to an “expanded” polynomial, written as just a sum of terms.Integer factorization for large integers appears to be a difficult problem. There is no known method to carry it out quickly. Its complexity is the basis of the assumed security of some public key cryptography algorithms, such as RSA.A matrix can also be factorized into a product of matrices of special types, for an application in which that form is convenient. One major example of this uses an orthogonal or unitary matrix, and a triangular matrix. There are different types: QR decomposition, LQ, QL, RQ, RZ.Another example is the factorization of a function as the composition of other functions having certain properties; for example, every function can be viewed as the composition of a surjective function with an injective function. This situation is generalized by factorization systems.