Solution Week 12 (12/2/02) Decreasing numbers First Solution: Let
... Second Solution: Let the first number you pick be x1 , the second x2 , the third x3 , and so on. There is a p2 = 1/2 chance that x2 < x1 . There is a p3 = 1/3! chance that x3 < x2 < x1 . There is a p4 = 1/4! chance that x4 < x3 < x2 < x1 , and so on. You must make at least two picks in this game. Th ...
... Second Solution: Let the first number you pick be x1 , the second x2 , the third x3 , and so on. There is a p2 = 1/2 chance that x2 < x1 . There is a p3 = 1/3! chance that x3 < x2 < x1 . There is a p4 = 1/4! chance that x4 < x3 < x2 < x1 , and so on. You must make at least two picks in this game. Th ...
Lecture09
... X will take a value no further than h from . These bounds apply to every random variable regardless of distribution, and so they are often quite crude. When we have information about the distribution, we can often do much better. g) Example: One study of heights in the U.S. concluded that women ha ...
... X will take a value no further than h from . These bounds apply to every random variable regardless of distribution, and so they are often quite crude. When we have information about the distribution, we can often do much better. g) Example: One study of heights in the U.S. concluded that women ha ...
Simulating Experiments
... Step 1: State the problem or describe the experiment Step 2: State the assumptions Step 3: Assign digits to represent outcomes Step 4: Simulate many repetitions. Step 5: State your conclusions. ...
... Step 1: State the problem or describe the experiment Step 2: State the assumptions Step 3: Assign digits to represent outcomes Step 4: Simulate many repetitions. Step 5: State your conclusions. ...
Repeated Trials Homework Solutions 1. What is the probability of
... i = 0, 1, 2, . . . , 12. You would then sum the terms 12 C i ...
... i = 0, 1, 2, . . . , 12. You would then sum the terms 12 C i ...
Honors Statistics Name______________________________ 3
... How many different ways are there to answer a 5 question multiple choice test if there are four choices for each question? ...
... How many different ways are there to answer a 5 question multiple choice test if there are four choices for each question? ...
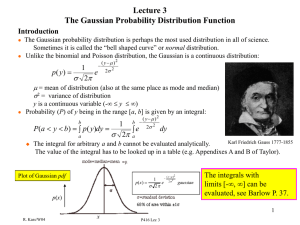
Gaussian Probability Distribution
... The Gaussian probability distribution is perhaps the most used distribution in all of science. Sometimes it is called the “bell shaped curve” or normal distribution. Unlike the binomial and Poisson distribution, the Gaussian is a continuous distribution: ...
... The Gaussian probability distribution is perhaps the most used distribution in all of science. Sometimes it is called the “bell shaped curve” or normal distribution. Unlike the binomial and Poisson distribution, the Gaussian is a continuous distribution: ...
Statistics-1
... The mean is an important indicator of quality The standard deviation is just as important Quality control to ensure minimum spread in properties Economic penalty of a ‘broad’ distribution “derating” to ‘guarantee’ a value ...
... The mean is an important indicator of quality The standard deviation is just as important Quality control to ensure minimum spread in properties Economic penalty of a ‘broad’ distribution “derating” to ‘guarantee’ a value ...
Notes on Kolmogorov Complexity
... Let hM i be a representation of a Turing machine M as a bit string, and for a bit string x let |x| be its length. We say that the pair (< M >, y) where M is a Turing machine and y is a bit string represents the bit string x if M on input y outputs x. We define the Kolmogorov complexity K(x) of a bit ...
... Let hM i be a representation of a Turing machine M as a bit string, and for a bit string x let |x| be its length. We say that the pair (< M >, y) where M is a Turing machine and y is a bit string represents the bit string x if M on input y outputs x. We define the Kolmogorov complexity K(x) of a bit ...
Independent and Dependent Events
... Example: Suppose you spin each of these two spinners. What is the probability of spinning an even number and a vowel? ...
... Example: Suppose you spin each of these two spinners. What is the probability of spinning an even number and a vowel? ...
PROBABILITY IS SYMMETRY
... of a sequence. Tigers are aggressive. Aggressiveness is not an attribute of atoms in tigers’ bodies. De Finetti: Observed frequency does not falsify a prior probability statement because it is based on different information. ...
... of a sequence. Tigers are aggressive. Aggressiveness is not an attribute of atoms in tigers’ bodies. De Finetti: Observed frequency does not falsify a prior probability statement because it is based on different information. ...
(1) Probability distribution: Consider the two probability density
... Find the fraction of the population that has died by age 20. (c) Find the fraction of the population that has died by age 80. (d) What is the mean lifetime in this population? (9) Quantum mechanics and electron clouds: Quantum mechanics tells us that we can never know with complete certainty where a ...
... Find the fraction of the population that has died by age 20. (c) Find the fraction of the population that has died by age 80. (d) What is the mean lifetime in this population? (9) Quantum mechanics and electron clouds: Quantum mechanics tells us that we can never know with complete certainty where a ...
An Introduction to Probability Theory - CAMP-TUM
... Probability theory is concerned with describing random phenomena mathematically. A basic concept is the probabilistic experiment. It is a repeatable experiment with the property that it is not possible to predict the outcome. Accordingly, we refer to a random quantity as the outcome of a probabilist ...
... Probability theory is concerned with describing random phenomena mathematically. A basic concept is the probabilistic experiment. It is a repeatable experiment with the property that it is not possible to predict the outcome. Accordingly, we refer to a random quantity as the outcome of a probabilist ...
1 - Art of Problem Solving
... 7. Five people stand at the vertices of a pentagon, throwing frisbees at each other. They have two frisbees, initially at adjacent vertices. At each step, each frisbee is thrown either to the left or to the right with equal probability. This process continues until one person is the target of two fr ...
... 7. Five people stand at the vertices of a pentagon, throwing frisbees at each other. They have two frisbees, initially at adjacent vertices. At each step, each frisbee is thrown either to the left or to the right with equal probability. This process continues until one person is the target of two fr ...
Infinite monkey theorem

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare.In this context, ""almost surely"" is a mathematical term with a precise meaning, and the ""monkey"" is not an actual monkey, but a metaphor for an abstract device that produces an endless random sequence of letters and symbols. One of the earliest instances of the use of the ""monkey metaphor"" is that of French mathematician Émile Borel in 1913, but the first instance may be even earlier. The relevance of the theorem is questionable—the probability of a universe full of monkeys typing a complete work such as Shakespeare's Hamlet is so tiny that the chance of it occurring during a period of time hundreds of thousands of orders of magnitude longer than the age of the universe is extremely low (but technically not zero). It should also be noted that real monkeys don't produce uniformly random output, which means that an actual monkey hitting keys for an infinite amount of time has no statistical certainty of ever producing any given text.Variants of the theorem include multiple and even infinitely many typists, and the target text varies between an entire library and a single sentence. The history of these statements can be traced back to Aristotle's On Generation and Corruption and Cicero's De natura deorum (On the Nature of the Gods), through Blaise Pascal and Jonathan Swift, and finally to modern statements with their iconic simians and typewriters. In the early 20th century, Émile Borel and Arthur Eddington used the theorem to illustrate the timescales implicit in the foundations of statistical mechanics.