GTS 111 Practice Final Exam
... (b) Is this situation a binomial experiment? Explain your reason. Answer: Yes because there is fixed number of trial n = 4. Each trial has two outcomes, prefer new razor, and not. If we let the successful outcome be ”prefer new razor” with p(S) = 0.1. Each trial is independent. (c) Find the probabi ...
... (b) Is this situation a binomial experiment? Explain your reason. Answer: Yes because there is fixed number of trial n = 4. Each trial has two outcomes, prefer new razor, and not. If we let the successful outcome be ”prefer new razor” with p(S) = 0.1. Each trial is independent. (c) Find the probabi ...
Chapter 14. More Fortran Elements: Random Number Generators
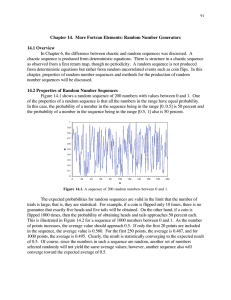
... sequences. That is, if the random number generator is given the same starting value (called the seed), then it will produce the same sequence every time. This behavior is known as a pseudorandom sequence, and it is useful for testing the Fortran code. The properties of a pseudo-random sequence are t ...
... sequences. That is, if the random number generator is given the same starting value (called the seed), then it will produce the same sequence every time. This behavior is known as a pseudorandom sequence, and it is useful for testing the Fortran code. The properties of a pseudo-random sequence are t ...
5 - Web4students
... 1) When randomly selecting jail inmates convicted of DWI (driving while intoxicated), the probability distribution for the number x of prior DWI sentences is as described in the accompanying table (based on data from the U.S. Department of Justice). ...
... 1) When randomly selecting jail inmates convicted of DWI (driving while intoxicated), the probability distribution for the number x of prior DWI sentences is as described in the accompanying table (based on data from the U.S. Department of Justice). ...
Sample Exam - Dalton State
... This is a take home exam that is to be completed by yourself and is due at the beginning of class on Nov. 1. There 30 short answer questions counting 3.4 points each Special note: Right answers are hard to argue with, but well set up wrong answers can count as much or more (consideration can flow in ...
... This is a take home exam that is to be completed by yourself and is due at the beginning of class on Nov. 1. There 30 short answer questions counting 3.4 points each Special note: Right answers are hard to argue with, but well set up wrong answers can count as much or more (consideration can flow in ...
Quasi-random numbers in stochastic finite element analysis
... The Latin Hypercube Sampling (LHS) method aims at generating pseudo-random numbers with a better uniformity over IM = [0, 1]M compared to MCS. The domain is divided into N equiprobable intervals or stratas, leading to a partition of IM in equiprobable subsets. Let us consider M independent uniform r ...
... The Latin Hypercube Sampling (LHS) method aims at generating pseudo-random numbers with a better uniformity over IM = [0, 1]M compared to MCS. The domain is divided into N equiprobable intervals or stratas, leading to a partition of IM in equiprobable subsets. Let us consider M independent uniform r ...
Some New Twists To Problems Involving The Gaussian Probability
... . Corresponding to the transmission of , the channel outputs the sequence ...
... . Corresponding to the transmission of , the channel outputs the sequence ...
WELL CALIBRATED, COHERENT FORECASTING SYSTEMS
... of laws governing observable phenomena, is viewed as an objective fact. Hence, the above mentioned idea of statistical inference might clash with the pragmatic position according to which the essential role of any scientific theory lies in making previsions about future possible facts. On the other ...
... of laws governing observable phenomena, is viewed as an objective fact. Hence, the above mentioned idea of statistical inference might clash with the pragmatic position according to which the essential role of any scientific theory lies in making previsions about future possible facts. On the other ...
Decidable fragments of first-order logic Decidable fragments of first
... Fix some 1-table T in T1 and assume that T has been assigned b n. to {b} during Step i of the construction of B Then we can extend T to an (l + 1)-table Text where Text is realized in A, ψ[1, 1, i3 , . . . , il+2 ] is true in Text for not necessarily pairwise distinct numbers i3 , . . . , il+2 in {1 ...
... Fix some 1-table T in T1 and assume that T has been assigned b n. to {b} during Step i of the construction of B Then we can extend T to an (l + 1)-table Text where Text is realized in A, ψ[1, 1, i3 , . . . , il+2 ] is true in Text for not necessarily pairwise distinct numbers i3 , . . . , il+2 in {1 ...
on-line
... • This gives generator with a period of m (length of sequence before repetition), and reasonable potency (measures certain dependencies among adjacent Xi.) • Also want bits of a to “have no obvious pattern” and pass certain other tests (see Knuth). ...
... • This gives generator with a period of m (length of sequence before repetition), and reasonable potency (measures certain dependencies among adjacent Xi.) • Also want bits of a to “have no obvious pattern” and pass certain other tests (see Knuth). ...
Chapter 8: Law of Large Numbers
... this probability finally exceeds any given degree of certainty; or whether the problem has, so to speak, its own asymptote—that is, whether some degree of certainty is given which one can never exceed.5 Bernoulli recognized the importance of this theorem, writing: Therefore, this is the problem whic ...
... this probability finally exceeds any given degree of certainty; or whether the problem has, so to speak, its own asymptote—that is, whether some degree of certainty is given which one can never exceed.5 Bernoulli recognized the importance of this theorem, writing: Therefore, this is the problem whic ...
Binomial and Geometric Distributions
... Binomial Experiments - experiments having all four conditions: 1. Each observation falls into one of two categories – we call them “success” or “failure.” (it is important to realize that success isn’t necessarily a positive. If for instance, our experiment is concerned with the number of people who ...
... Binomial Experiments - experiments having all four conditions: 1. Each observation falls into one of two categories – we call them “success” or “failure.” (it is important to realize that success isn’t necessarily a positive. If for instance, our experiment is concerned with the number of people who ...
Infinite monkey theorem

The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare.In this context, ""almost surely"" is a mathematical term with a precise meaning, and the ""monkey"" is not an actual monkey, but a metaphor for an abstract device that produces an endless random sequence of letters and symbols. One of the earliest instances of the use of the ""monkey metaphor"" is that of French mathematician Émile Borel in 1913, but the first instance may be even earlier. The relevance of the theorem is questionable—the probability of a universe full of monkeys typing a complete work such as Shakespeare's Hamlet is so tiny that the chance of it occurring during a period of time hundreds of thousands of orders of magnitude longer than the age of the universe is extremely low (but technically not zero). It should also be noted that real monkeys don't produce uniformly random output, which means that an actual monkey hitting keys for an infinite amount of time has no statistical certainty of ever producing any given text.Variants of the theorem include multiple and even infinitely many typists, and the target text varies between an entire library and a single sentence. The history of these statements can be traced back to Aristotle's On Generation and Corruption and Cicero's De natura deorum (On the Nature of the Gods), through Blaise Pascal and Jonathan Swift, and finally to modern statements with their iconic simians and typewriters. In the early 20th century, Émile Borel and Arthur Eddington used the theorem to illustrate the timescales implicit in the foundations of statistical mechanics.