Exam 1 - NIU Math Department
... (1) Print your name and student number (ZID) above. (2) Make certain that your test has all five (5) different sheets (including the cover page). (3) You must SHOW YOUR WORK in order to get credit. (4) Clearly indicate your answer to each problem BY CIRCLING IT. (5) The point value of each problem i ...
... (1) Print your name and student number (ZID) above. (2) Make certain that your test has all five (5) different sheets (including the cover page). (3) You must SHOW YOUR WORK in order to get credit. (4) Clearly indicate your answer to each problem BY CIRCLING IT. (5) The point value of each problem i ...
Cross-mining Binary and Numerical Attributes
... together [1]. After several years of research many efficient algorithms have been developed to mine frequent itemsets, e.g. Apriori [2] or FP-growth [6] among others. Other variations of the problem are mining frequent closed sets [18] or mining maximal frequent sets [3]. In all cases, finding such ...
... together [1]. After several years of research many efficient algorithms have been developed to mine frequent itemsets, e.g. Apriori [2] or FP-growth [6] among others. Other variations of the problem are mining frequent closed sets [18] or mining maximal frequent sets [3]. In all cases, finding such ...
Math 122 Lecture 1: Antiderivatives
... = f (x ) dx If F is an antiderivative of the function f , then one possible solution is y = F (x ). The general solution is the most general antiderivative of the function f , that is, y = F (x ) + C where C is an arbitrary constant. ...
... = f (x ) dx If F is an antiderivative of the function f , then one possible solution is y = F (x ). The general solution is the most general antiderivative of the function f , that is, y = F (x ) + C where C is an arbitrary constant. ...
PHY 231 HW6 F=ma View Basic/Answers HW6 F=ma Begin Date: 2
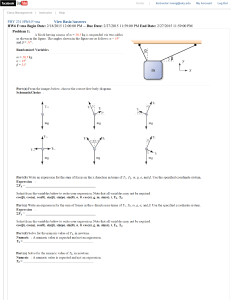
... Full solution not currently available at this time. Cranes use a system of two pulleys to provide mechanical advantage, which reduces the force they need to apply to lift a particular weight (two such possible configurations are shown in the figure). A crane is attempting to lift a compact car with ...
... Full solution not currently available at this time. Cranes use a system of two pulleys to provide mechanical advantage, which reduces the force they need to apply to lift a particular weight (two such possible configurations are shown in the figure). A crane is attempting to lift a compact car with ...
MATH 5a EXTRA PRACTICE FOR EXAM 2 1. Solve the following
... (c) Find the domain of f (x). Write your answer in interval notation. (d) Find the range of f (x). Write your answer in interval notation. (e) On what interval(s) is the graph of f (x) increasing? Write your answer in interval notation. (f) On what interval(s) is the graph of f (x) positive? Write y ...
... (c) Find the domain of f (x). Write your answer in interval notation. (d) Find the range of f (x). Write your answer in interval notation. (e) On what interval(s) is the graph of f (x) increasing? Write your answer in interval notation. (f) On what interval(s) is the graph of f (x) positive? Write y ...
satellite frequency assignments using transiently chaotic neural
... FAP, we focus on minimization of system interference for fixed frequency assignments in satellite communications. Interference in satellite communications depends on transmitter power, channel loss, receiver sensitivity, and antenna gains. Frequency rearrangements are an effective complement alongs ...
... FAP, we focus on minimization of system interference for fixed frequency assignments in satellite communications. Interference in satellite communications depends on transmitter power, channel loss, receiver sensitivity, and antenna gains. Frequency rearrangements are an effective complement alongs ...
group communication
... Build an agenda Hold routine meetings Choose a leader A group can be 3-15 in membership; but 5-8 is best. Identify problems and solutions ...
... Build an agenda Hold routine meetings Choose a leader A group can be 3-15 in membership; but 5-8 is best. Identify problems and solutions ...
Mathematical optimization

In mathematics, computer science and operations research, mathematical optimization (alternatively, optimization or mathematical programming) is the selection of a best element (with regard to some criteria) from some set of available alternatives.In the simplest case, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations comprises a large area of applied mathematics. More generally, optimization includes finding ""best available"" values of some objective function given a defined domain (or a set of constraints), including a variety of different types of objective functions and different types of domains.