Counting Inversions, Offline Orthogonal Range Counting, and Related Problems Timothy M. Chan
... 1.3 Applications. Though our solution idea is quite sible to achieve query time O(lg n/ lg lg n) with space simple, the end result remains surprising. In fact, more O(n) [JMS04]. powerful instantiations of this basic idea yield a handful Given this precise understanding, it now makes of improved al ...
... 1.3 Applications. Though our solution idea is quite sible to achieve query time O(lg n/ lg lg n) with space simple, the end result remains surprising. In fact, more O(n) [JMS04]. powerful instantiations of this basic idea yield a handful Given this precise understanding, it now makes of improved al ...
A High-Performance Multi-Element Processing Framework on GPUs
... for the generality of our framework. Second, linear algebra packages have been the most widely-used components in scientific computing applications and its efficiency is critical ...
... for the generality of our framework. Second, linear algebra packages have been the most widely-used components in scientific computing applications and its efficiency is critical ...
PDF 2 Heat Equation
... for some scalar λ and T to be a solution of the ODE −T 0 = kλT. We have given some examples above of how to solve the eigenvalue problem. Once we have solved the eigenvalue problem, we need to solve our equation for T . In particular, for any scalar λ, the solution of the ODE for T is given by T (t) ...
... for some scalar λ and T to be a solution of the ODE −T 0 = kλT. We have given some examples above of how to solve the eigenvalue problem. Once we have solved the eigenvalue problem, we need to solve our equation for T . In particular, for any scalar λ, the solution of the ODE for T is given by T (t) ...
price-based market clearing under marginal pricing: a
... [6] is the proposal of an equivalent single-level mixedinteger linear formulation based on the Karush-KuhnTucker (KKT) optimality conditions, duality theory, and integer algebra results. The main advantages of expressing the original bilevel optimization as an equivalent single-level mixed-integer l ...
... [6] is the proposal of an equivalent single-level mixedinteger linear formulation based on the Karush-KuhnTucker (KKT) optimality conditions, duality theory, and integer algebra results. The main advantages of expressing the original bilevel optimization as an equivalent single-level mixed-integer l ...
Geocentric solution to 3-body prob
... are: the sun, the earth, and a third body, of negligible mass, that appear at rest relative to those two bodies. Fundamentally, we are looking to answer this question: “At what locations is the orbital speed of the negligible-mass body zero with respect to both the sun and earth?” As a point of term ...
... are: the sun, the earth, and a third body, of negligible mass, that appear at rest relative to those two bodies. Fundamentally, we are looking to answer this question: “At what locations is the orbital speed of the negligible-mass body zero with respect to both the sun and earth?” As a point of term ...
Uniqueness of solutions to the Laplace and Poisson equations
... Cauchy boundary conditions. In such an exceptional case, the solution to the Dirichlet problem is also the solution to the Cauchy problem, and the solution is unique. However, in general there is no reason to expect the resulting ∂u/∂n for all ~ x ∈ S to be consistent with the original Cauchy bounda ...
... Cauchy boundary conditions. In such an exceptional case, the solution to the Dirichlet problem is also the solution to the Cauchy problem, and the solution is unique. However, in general there is no reason to expect the resulting ∂u/∂n for all ~ x ∈ S to be consistent with the original Cauchy bounda ...
part_3
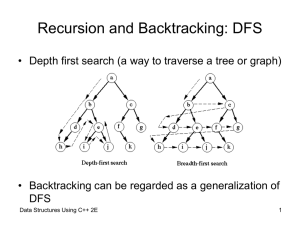
... Puzzle (cont’d.) • Backtracking algorithm – Find problem solutions by constructing partial solutions – Ensures partial solution does not violate requirements – Extends partial solution toward completion – If partial solution does not lead to a solution (dead end) • Algorithm backs up • Removes most ...
... Puzzle (cont’d.) • Backtracking algorithm – Find problem solutions by constructing partial solutions – Ensures partial solution does not violate requirements – Extends partial solution toward completion – If partial solution does not lead to a solution (dead end) • Algorithm backs up • Removes most ...