Vector Spaces
... but the scalar multiplication properties may or may not be satisfied. If V is a vector space, then we have to prove that all 10 properties are satisfied. However, if even one property fails, then V is NOT a vector space. Therefore, it is beneficial to start with the properties that you think may fai ...
... but the scalar multiplication properties may or may not be satisfied. If V is a vector space, then we have to prove that all 10 properties are satisfied. However, if even one property fails, then V is NOT a vector space. Therefore, it is beneficial to start with the properties that you think may fai ...
Objective#1: Find the value of the six trigonometric functions
... Objective#1: Find the value of the six trigonometric functions. Objective #2: Find the value of the six trigonometric functions of an angle in standard position given a point on its terminal side. The Unit Circle 9 A unit circle is a circle with radius 1 and center (0,0). 9 The unit circle can be us ...
... Objective#1: Find the value of the six trigonometric functions. Objective #2: Find the value of the six trigonometric functions of an angle in standard position given a point on its terminal side. The Unit Circle 9 A unit circle is a circle with radius 1 and center (0,0). 9 The unit circle can be us ...
CONTINUOUS SELECTIONS AND FIXED POINTS OF MULTI
... X into the power set 2Y of Y . Let T −1 : Y → 2X be defined by the condition that x ∈ T −1 y if and only if y ∈ T (x). Recall that (a) T is said to be closed if its graph Gr (T ) = {(x, y) : x ∈ X, y ∈ T (x)} is closed in the product space X × Y ; (b) T is said to be upper semicontinuous (in short, ...
... X into the power set 2Y of Y . Let T −1 : Y → 2X be defined by the condition that x ∈ T −1 y if and only if y ∈ T (x). Recall that (a) T is said to be closed if its graph Gr (T ) = {(x, y) : x ∈ X, y ∈ T (x)} is closed in the product space X × Y ; (b) T is said to be upper semicontinuous (in short, ...
PRECALCULUS MA2090 - SUNY Old Westbury
... their graphs. This course is designed primarily for students who wish to take MA2310 Calculus & Analytic Geometry I. COURSE OBJECTIVES: ...
... their graphs. This course is designed primarily for students who wish to take MA2310 Calculus & Analytic Geometry I. COURSE OBJECTIVES: ...
Document
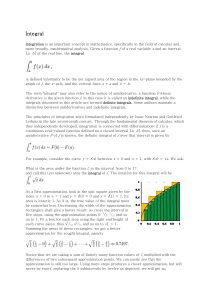
... Produces an integral that is expressed entirely in terms of u and du, (may not OK) Step 2 If OK in Step 1, then try to evaluate the resolution integral in terms of u, (may not OK) Step 3 If OK in Step 2, then replace u by g(x) to express your final answer in term of x. ...
... Produces an integral that is expressed entirely in terms of u and du, (may not OK) Step 2 If OK in Step 1, then try to evaluate the resolution integral in terms of u, (may not OK) Step 3 If OK in Step 2, then replace u by g(x) to express your final answer in term of x. ...
Math 441 Topology Fall 2012 Metric Spaces by John M. Lee This
... now be defined exactly as we did for maps between Euclidean spaces: We say that f is continuous if for every a ∈ X and every ε > 0, there exists δ > 0 such that for all x ∈ X with d(x, a) < δ, we have ρ(f (x), f (a)) < ε. Example 3.4. If X is a subset of Rn with the Euclidean metric, then continuity ...
... now be defined exactly as we did for maps between Euclidean spaces: We say that f is continuous if for every a ∈ X and every ε > 0, there exists δ > 0 such that for all x ∈ X with d(x, a) < δ, we have ρ(f (x), f (a)) < ε. Example 3.4. If X is a subset of Rn with the Euclidean metric, then continuity ...
MATH 307 Subspaces
... Example 3. Let V = R and let W = {( x , y , z ) : z = 0} . Then (0, 0, 0) ∈ W ; so W is nonempty. For vectors (x1, y€1, 0) and (x 2 , y 2 , 0) in W and for any scalar c , we have ...
... Example 3. Let V = R and let W = {( x , y , z ) : z = 0} . Then (0, 0, 0) ∈ W ; so W is nonempty. For vectors (x1, y€1, 0) and (x 2 , y 2 , 0) in W and for any scalar c , we have ...
Math 535 - General Topology Fall 2012 Homework 1 Solutions
... Let Cα be a family of subsets that are either finite or all of X. Then the intersection α Cα is finite (if at least one Cα is finite) or all of X (if all Cα are X). 3. Let C, C 0 be subsets that are either finite or all of X. Then the union C ∪ C 0 is finite (if both C and C 0 are finite) or all of ...
... Let Cα be a family of subsets that are either finite or all of X. Then the intersection α Cα is finite (if at least one Cα is finite) or all of X (if all Cα are X). 3. Let C, C 0 be subsets that are either finite or all of X. Then the union C ∪ C 0 is finite (if both C and C 0 are finite) or all of ...
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue (Dunford & Schwartz 1958, III.3), although according to the Bourbaki group (Bourbaki 1987) they were first introduced by Frigyes Riesz (Riesz 1910).Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces.Lebesgue spaces have applications in physics, statistics, finance, engineering, and other disciplines.