PDF file
... The Tychonoff plank X = (ω1 + 1 × ω + 1) \ {hω1 , ωi} is a famous example of a T3 1 -space which is not normal, see [1]. It is also a famous example of the ...
... The Tychonoff plank X = (ω1 + 1 × ω + 1) \ {hω1 , ωi} is a famous example of a T3 1 -space which is not normal, see [1]. It is also a famous example of the ...
INVARIANCE OF DOMAIN AND THE JORDAN CURVE THEOREM
... Remark 2.10. In fact, without much effort, one can show that a space is simply connected if and only if the fundamental group of the space is trivial. This gives an alternative definition of simply connected space. 3. Covering Spaces and the Fundamental Group of S 1 In algebraic topology, the notion ...
... Remark 2.10. In fact, without much effort, one can show that a space is simply connected if and only if the fundamental group of the space is trivial. This gives an alternative definition of simply connected space. 3. Covering Spaces and the Fundamental Group of S 1 In algebraic topology, the notion ...
TOPOLOGY IN A CATEGORY: COMPACTNESS 0 – Introduction
... economical fashion. Topologically-motivated ideas may therefore be applied directly to categories of other branches of mathematics, but we hope that even readers only interested in point-set topology may benefit from implementing the categorical approach. It has been observed by several authors that ...
... economical fashion. Topologically-motivated ideas may therefore be applied directly to categories of other branches of mathematics, but we hope that even readers only interested in point-set topology may benefit from implementing the categorical approach. It has been observed by several authors that ...
13b.pdf
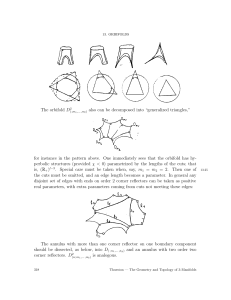
... (b) For each elliptic point or corner reflector of order n, an integer 0 ≤ k < n which specifies the local structure. Above an elliptic point, the Zn action on Ũ × S 1 is generated by a 1/n rotation of the disk U and a k/n rotation of the fiber S 1 . Above a corner reflector, the Dn action on Ũ × ...
... (b) For each elliptic point or corner reflector of order n, an integer 0 ≤ k < n which specifies the local structure. Above an elliptic point, the Zn action on Ũ × S 1 is generated by a 1/n rotation of the disk U and a k/n rotation of the fiber S 1 . Above a corner reflector, the Dn action on Ũ × ...
Covering Maps and the Monodromy Theorem
... Proof The map p: X̃ → X is a covering map; therefore there exists an open cover U of X such that each open set U belonging to X is evenly covered by the map p. Now the collection consisting of the preimages γ −1 (U ) of the open sets U belonging to U is an open cover of the interval [0, 1]. But [0, ...
... Proof The map p: X̃ → X is a covering map; therefore there exists an open cover U of X such that each open set U belonging to X is evenly covered by the map p. Now the collection consisting of the preimages γ −1 (U ) of the open sets U belonging to U is an open cover of the interval [0, 1]. But [0, ...
First-order difference equation
... 1. τ −1 : E → D is a topological conjugacy. 2. τ ◦ f n = g n ◦ τ for all n ∈ N. 3. p is a periodic point of f with least period n iff τ (p) is a periodic point of g with least period n. 4. If p is a periodic point of f with stable set W s (p), then the stable set of τ (p) is τ (W s (p)). 5. The peri ...
... 1. τ −1 : E → D is a topological conjugacy. 2. τ ◦ f n = g n ◦ τ for all n ∈ N. 3. p is a periodic point of f with least period n iff τ (p) is a periodic point of g with least period n. 4. If p is a periodic point of f with stable set W s (p), then the stable set of τ (p) is τ (W s (p)). 5. The peri ...
General topology
In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology. Another name for general topology is point-set topology.The fundamental concepts in point-set topology are continuity, compactness, and connectedness: Continuous functions, intuitively, take nearby points to nearby points. Compact sets are those that can be covered by finitely many sets of arbitrarily small size. Connected sets are sets that cannot be divided into two pieces that are far apart. The words 'nearby', 'arbitrarily small', and 'far apart' can all be made precise by using open sets, as described below. If we change the definition of 'open set', we change what continuous functions, compact sets, and connected sets are. Each choice of definition for 'open set' is called a topology. A set with a topology is called a topological space.Metric spaces are an important class of topological spaces where distances can be assigned a number called a metric. Having a metric simplifies many proofs, and many of the most common topological spaces are metric spaces.