Locally compact perfectly normal spaces may all be paracompact
... force PFA(S) and lastly force with S. The iteration of these three forcings has the κchain condition and is of size κ, so we have established that normal first countable spaces that are < κ-collectionwise Hausdorff are collectionwise Hausdorff. It is clear that the straightforward iteration to produ ...
... force PFA(S) and lastly force with S. The iteration of these three forcings has the κchain condition and is of size κ, so we have established that normal first countable spaces that are < κ-collectionwise Hausdorff are collectionwise Hausdorff. It is clear that the straightforward iteration to produ ...
Three Questions on Special Homeomorphisms on Subgroups of $ R
... Section 2 too. As mentioned earlier, the results leading to the above questions hold not only for σ-compact subgroups of R but also for all zero-dimensional subgroups with the property that every two non-empty open sets are homeomorphic. As shown in [4], this property need not be present in a dense ...
... Section 2 too. As mentioned earlier, the results leading to the above questions hold not only for σ-compact subgroups of R but also for all zero-dimensional subgroups with the property that every two non-empty open sets are homeomorphic. As shown in [4], this property need not be present in a dense ...
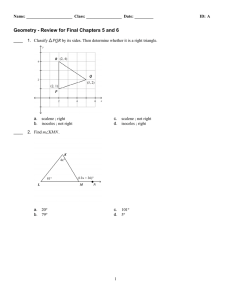
ExamView - geometry review for final chapters 5 and 6 .tst
... 51. yes; Because point P is equidistant from L and M , point P is on the perpendicular bisector of LM by the Converse of the Perpendicular Bisector Theorem. Also, LN ≅ MN , so PN is a bisector of LM . Because P can only be on one of the bisectors, PN is the perpendicular bisector of LM . 52. The fir ...
... 51. yes; Because point P is equidistant from L and M , point P is on the perpendicular bisector of LM by the Converse of the Perpendicular Bisector Theorem. Also, LN ≅ MN , so PN is a bisector of LM . Because P can only be on one of the bisectors, PN is the perpendicular bisector of LM . 52. The fir ...
Non-Euclidean Geometry Unit
... along them. Therefore, lines in spherical geometry are Great Circles. A Great Circle is the largest circle that can be drawn on a sphere. The longitude lines and the equator are Great Circles of the Earth. Latitude lines, except for the equator, are not Great Circles. Great Circles are lines that di ...
... along them. Therefore, lines in spherical geometry are Great Circles. A Great Circle is the largest circle that can be drawn on a sphere. The longitude lines and the equator are Great Circles of the Earth. Latitude lines, except for the equator, are not Great Circles. Great Circles are lines that di ...
3-manifold

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. Intuitively, a 3-manifold can be thought of as a possible shape of the universe. Just like a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.