Topology of the Real Numbers
... that are the crucial ones. Chapter 13 has further explanation. 5.3.1. Sequential definition. Intuitively, a compact set confines every sequence of points in the set so much that the sequence must accumulate at some point of the set. This implies that a subsequence converges to an accumulation point ...
... that are the crucial ones. Chapter 13 has further explanation. 5.3.1. Sequential definition. Intuitively, a compact set confines every sequence of points in the set so much that the sequence must accumulate at some point of the set. This implies that a subsequence converges to an accumulation point ...
MAT327H1: Introduction to Topology
... the smallest closed set containing A . Proposition x ∈ Å if and only if there exists an open U such that x ∈ U ⊂ A . Proof: ( ⇒ ) x ∈ Å , take U = Å . ( ⇐ ) If x ∈ U ⊂ A , U open, then Å ∪U = Å is open and contained in A . So U ⊂ Å and x∈ Å . Proposition x ∈ A if and only if for all open U , ...
... the smallest closed set containing A . Proposition x ∈ Å if and only if there exists an open U such that x ∈ U ⊂ A . Proof: ( ⇒ ) x ∈ Å , take U = Å . ( ⇐ ) If x ∈ U ⊂ A , U open, then Å ∪U = Å is open and contained in A . So U ⊂ Å and x∈ Å . Proposition x ∈ A if and only if for all open U , ...
PROPERTIES For any numbers a, b, c, and d: (Arithmetic) 1
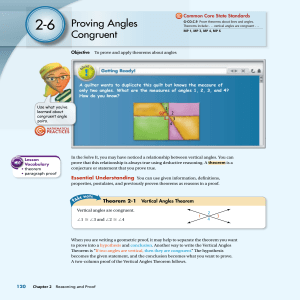
... 12. Corresponding Angles Postulate, or CA Postulate: If two parallel lines are cut by a transversal, then the corresponding angles are congruent. Conversely, if two lines are cut by a transversal forming congruent corresponding angles, then the lines are parallel. 13. SSS Congruence Postulate: If th ...
... 12. Corresponding Angles Postulate, or CA Postulate: If two parallel lines are cut by a transversal, then the corresponding angles are congruent. Conversely, if two lines are cut by a transversal forming congruent corresponding angles, then the lines are parallel. 13. SSS Congruence Postulate: If th ...
polygon - Mona Shores Blogs
... polygons based on the number of sides. Identify the components of a polygon. Use the sum of the interior angles of a quadrilateral. ...
... polygons based on the number of sides. Identify the components of a polygon. Use the sum of the interior angles of a quadrilateral. ...
Embedding Locally Compact Semigroups into Groups
... Finally we show that S homeomorphically embeds onto an open subset of G. Let s ∈ S and let V be an open neighborhood of s in S . Then xV is an open neighborhood of xs and so there exists U ∈ Nx such that U s ⊆ xV , i.e., x−1 U s ⊆ V (in G). Since x−1 U s is open in G, contains s, and is contained in ...
... Finally we show that S homeomorphically embeds onto an open subset of G. Let s ∈ S and let V be an open neighborhood of s in S . Then xV is an open neighborhood of xs and so there exists U ∈ Nx such that U s ⊆ xV , i.e., x−1 U s ⊆ V (in G). Since x−1 U s is open in G, contains s, and is contained in ...
Grey subsets of Polish spaces
... automatic continuity property, i.e., any group homomorphism with source Aut([0, 1], λ) and taking values in a separable topological group must be continuous. This automatic continuity theorem was given a shorter proof, which also involves the use of the uniform metric and the pointwise convergence t ...
... automatic continuity property, i.e., any group homomorphism with source Aut([0, 1], λ) and taking values in a separable topological group must be continuous. This automatic continuity theorem was given a shorter proof, which also involves the use of the uniform metric and the pointwise convergence t ...
Chapter 3 Topological and Metric Spaces
... The distance or more generally the notion of nearness is closely related with everyday life of any human being so it is natural that in mathematics it plays also an important role which might be considered in certain periods even as starring role. Despite the historical course of affairs we start th ...
... The distance or more generally the notion of nearness is closely related with everyday life of any human being so it is natural that in mathematics it plays also an important role which might be considered in certain periods even as starring role. Despite the historical course of affairs we start th ...
3-manifold

In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. Intuitively, a 3-manifold can be thought of as a possible shape of the universe. Just like a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.