1. Lecture 4, February 21 1.1. Open immersion. Let (X,O X) be a
... As a consequence of the lemma, we have that the sets V (I) form the closed sets for the Zariski topology on Proj(S). In particular we have that the open sets D+ (f ) = Proj(S) \ V (f ), with homogeneous elements f , form a basis for the topology on Proj(S). Lemma 1.7. Let f ∈ S+ be a homogeneous ele ...
... As a consequence of the lemma, we have that the sets V (I) form the closed sets for the Zariski topology on Proj(S). In particular we have that the open sets D+ (f ) = Proj(S) \ V (f ), with homogeneous elements f , form a basis for the topology on Proj(S). Lemma 1.7. Let f ∈ S+ be a homogeneous ele ...
Group Theory: Basic Concepts Contents 1 Definitions
... • If the order of a is infinite, hai = Z. ⋆ More generally, if T is any subset of G, hT i is defined to be the smallest subgroup containing T as a subset, the subgroup generated by T . If hT i = G, one says that T , or the elements in T , generate G. The {} denoting a set can be omitted; h{a, b}i ca ...
... • If the order of a is infinite, hai = Z. ⋆ More generally, if T is any subset of G, hT i is defined to be the smallest subgroup containing T as a subset, the subgroup generated by T . If hT i = G, one says that T , or the elements in T , generate G. The {} denoting a set can be omitted; h{a, b}i ca ...
Topology - Homework Sets 8 and 9
... subspaces. Show that there exist disjoint open sets U and V such that A ⊂ U, ...
... subspaces. Show that there exist disjoint open sets U and V such that A ⊂ U, ...
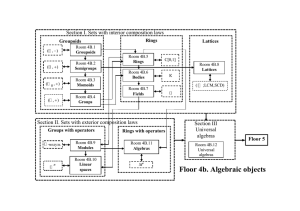
Section I. SETS WITH INTERIOR COMPOSITION LAWS
... Answer. If е1 and е2 are units, then е1е2 = е1, е1е2 = е2. So е1 = е2, namely the unit is unique. The unit of the additional monoid is called zero. Considered numerical semigroups are monoids with the exception of the additional semigroup of natural numbers. The unit for monoids ((Y),) and ((Y) ...
... Answer. If е1 and е2 are units, then е1е2 = е1, е1е2 = е2. So е1 = е2, namely the unit is unique. The unit of the additional monoid is called zero. Considered numerical semigroups are monoids with the exception of the additional semigroup of natural numbers. The unit for monoids ((Y),) and ((Y) ...
Pseudouniform topologies on C(X) given by ideals
... This section contains the basic definitions and notations that will be followed in this paper. All topological concepts that are not defined here should be understood as in T [2] except for the following: a uniformity U on a set X does not have to satisfy U = {(x, x) : x ∈ X}. Therefore, uniform spa ...
... This section contains the basic definitions and notations that will be followed in this paper. All topological concepts that are not defined here should be understood as in T [2] except for the following: a uniformity U on a set X does not have to satisfy U = {(x, x) : x ∈ X}. Therefore, uniform spa ...