Sections 3.1-3.2
... The m n zero matrix has all its entries equal to zero. It is denoted by 0 mn or if it is clear from the context just by 0. The matrix entries aij in an m n matrix for which i j are called diagonal elements; all of them make up the (main) diagonal of a matrix. A diagonal matrix is a square matrix ...
... The m n zero matrix has all its entries equal to zero. It is denoted by 0 mn or if it is clear from the context just by 0. The matrix entries aij in an m n matrix for which i j are called diagonal elements; all of them make up the (main) diagonal of a matrix. A diagonal matrix is a square matrix ...
The matrix of a linear operator in a pair of ordered bases∗
... matrix (2) has m rows and n columns. Because of this, we say that it has the order m × n. The matrix (2) may be written in an abbreviated form as A = (aij ). Example 1.. Let D : P 3 → P 2 be a linear operator that assigns to each polynomial its derivative, (e) = (x3 , x2 , x, 1) the basis for P 3 an ...
... matrix (2) has m rows and n columns. Because of this, we say that it has the order m × n. The matrix (2) may be written in an abbreviated form as A = (aij ). Example 1.. Let D : P 3 → P 2 be a linear operator that assigns to each polynomial its derivative, (e) = (x3 , x2 , x, 1) the basis for P 3 an ...
Linear Algebra Libraries: BLAS, LAPACK - svmoore
... • A LAPACK subroutine name is in the form pmmaaa, where: – p is a one-letter code denoting the type of numerical constants used. S, D stand for real floating point arithmetic respectively in single and double precision, while C and Z stand for complex arithmetic with respectively single and double p ...
... • A LAPACK subroutine name is in the form pmmaaa, where: – p is a one-letter code denoting the type of numerical constants used. S, D stand for real floating point arithmetic respectively in single and double precision, while C and Z stand for complex arithmetic with respectively single and double p ...
Elementary Linear Algebra
... A matrix can be subdivided or partitioned into smaller matrices by inserting horizontal and vertical rules between selected rows and columns. For example, below are three possible partitions of a general 3 ×4 matrix A . ...
... A matrix can be subdivided or partitioned into smaller matrices by inserting horizontal and vertical rules between selected rows and columns. For example, below are three possible partitions of a general 3 ×4 matrix A . ...
Using matrix inverses and Mathematica to solve systems of equations
... If the determinant of an n × n matrix, A, is non-zero, then the matrix A has an inverse matrix, A−1 . We will not study how to construct the inverses of such matrices for n ≥ 3 in this course, because of time constraints. One can find the inverse either by an algebraic formula as with 2 × 2 matrices ...
... If the determinant of an n × n matrix, A, is non-zero, then the matrix A has an inverse matrix, A−1 . We will not study how to construct the inverses of such matrices for n ≥ 3 in this course, because of time constraints. One can find the inverse either by an algebraic formula as with 2 × 2 matrices ...
Sinha, B. K. and Saha, Rita.Optimal Weighing Designs with a String Property."
... (ii) The column-totals (through all or any subset of consecutive rows) are essentially (0 ,±l) - not all being O's. (iii) If a certain collli~-total is +1(-1), the first nonzero entry in that column is +1(-1); if a certain column-total is 0, the first non-zero entry in that column is either +1 or -1 ...
... (ii) The column-totals (through all or any subset of consecutive rows) are essentially (0 ,±l) - not all being O's. (iii) If a certain collli~-total is +1(-1), the first nonzero entry in that column is +1(-1); if a certain column-total is 0, the first non-zero entry in that column is either +1 or -1 ...
univariate case
... Although the condition above requires the nonnegativity of 2n − 1 expressions, it is possible to do the same by checking only n inequalities: Theorem 16 (e.g. [HJ95, p. 403]). A real n × n symmetric matrix A is positive semidefinite if and only if all the coefficients ci of its characteristic polynomia ...
... Although the condition above requires the nonnegativity of 2n − 1 expressions, it is possible to do the same by checking only n inequalities: Theorem 16 (e.g. [HJ95, p. 403]). A real n × n symmetric matrix A is positive semidefinite if and only if all the coefficients ci of its characteristic polynomia ...
Outline of the Pre-session Tianxi Wang
... Definition. A row of a matrix has k-leading zeros if the first k elements of the row are all zeros and the k + 1 element is non-zero. A matrix is in row echelon form if each row has more leading zeros then the row proceeding it. With elementary row operations we can always go from a matrix A to its ...
... Definition. A row of a matrix has k-leading zeros if the first k elements of the row are all zeros and the k + 1 element is non-zero. A matrix is in row echelon form if each row has more leading zeros then the row proceeding it. With elementary row operations we can always go from a matrix A to its ...
Solutions for Assignment 2
... Therefore we have the following cases: 1. if 2b−c−a 6= 0 then the RREF of the augmented matrix has an inconsistant row, therefore, the system has no solution. 2. If 2b − c − a = 0 then {(b − 2a + s, a − 2s, s) : s ∈ R} is the solution set for the system. So the system has infinitely many solutions ...
... Therefore we have the following cases: 1. if 2b−c−a 6= 0 then the RREF of the augmented matrix has an inconsistant row, therefore, the system has no solution. 2. If 2b − c − a = 0 then {(b − 2a + s, a − 2s, s) : s ∈ R} is the solution set for the system. So the system has infinitely many solutions ...
BSS 797: Principles of Parallel Computing
... Therefore, each processor is given n/P rows of the matrix and the entire column of the vector. The actual implementation is easy to do. Performance analysis for this row partition: Each processor multiplies a matrix of (n/P)*n with a vector n*1. The cost is Tm(P, n) = c n * (n/P). The time to distri ...
... Therefore, each processor is given n/P rows of the matrix and the entire column of the vector. The actual implementation is easy to do. Performance analysis for this row partition: Each processor multiplies a matrix of (n/P)*n with a vector n*1. The cost is Tm(P, n) = c n * (n/P). The time to distri ...
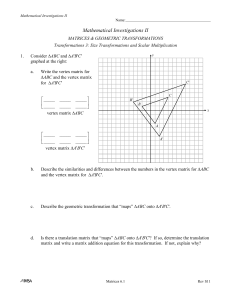
6.4 Dilations
... different sizes (though they do have the same shape; such triangles are called similar triangles). This type of transformation is called a dilation. The dilation in problem #1 is sometimes referred to as D2 since the coordinates of the image triangle, A'B'C', are all double those of the original tr ...
... different sizes (though they do have the same shape; such triangles are called similar triangles). This type of transformation is called a dilation. The dilation in problem #1 is sometimes referred to as D2 since the coordinates of the image triangle, A'B'C', are all double those of the original tr ...
Jordan normal form
In linear algebra, a Jordan normal form (often called Jordan canonical form)of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called a Jordan matrix, representing the operator with respect to some basis. Such matrix has each non-zero off-diagonal entry equal to 1, immediately above the main diagonal (on the superdiagonal), and with identical diagonal entries to the left and below them. If the vector space is over a field K, then a basis with respect to which the matrix has the required form exists if and only if all eigenvalues of the matrix lie in K, or equivalently if the characteristic polynomial of the operator splits into linear factors over K. This condition is always satisfied if K is the field of complex numbers. The diagonal entries of the normal form are the eigenvalues of the operator, with the number of times each one occurs being given by its algebraic multiplicity.If the operator is originally given by a square matrix M, then its Jordan normal form is also called the Jordan normal form of M. Any square matrix has a Jordan normal form if the field of coefficients is extended to one containing all the eigenvalues of the matrix. In spite of its name, the normal form for a given M is not entirely unique, as it is a block diagonal matrix formed of Jordan blocks, the order of which is not fixed; it is conventional to group blocks for the same eigenvalue together, but no ordering is imposed among the eigenvalues, nor among the blocks for a given eigenvalue, although the latter could for instance be ordered by weakly decreasing size.The Jordan–Chevalley decomposition is particularly simple with respect to a basis for which the operator takes its Jordan normal form. The diagonal form for diagonalizable matrices, for instance normal matrices, is a special case of the Jordan normal form.The Jordan normal form is named after Camille Jordan.