Exam 1 solutions
... 1.(5pts) Let A be a 6 × 5 matrix. What must a and b be in order to define T : Ra → Rb by T (x) = Ax? If we are trying to compute Ax then x must be a length 5 vector. The result of Ax is a length 6 vector. So a = 5 and b = 6. 2.(5pts) Give an example of a 2 × 2 matrix A which has the following three ...
... 1.(5pts) Let A be a 6 × 5 matrix. What must a and b be in order to define T : Ra → Rb by T (x) = Ax? If we are trying to compute Ax then x must be a length 5 vector. The result of Ax is a length 6 vector. So a = 5 and b = 6. 2.(5pts) Give an example of a 2 × 2 matrix A which has the following three ...
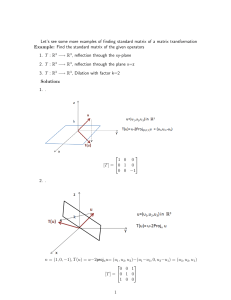
Find the standard matrix of the gi
... Definition: A matrix transformation T : Rn → Rm is said to be one-to-one if T maps distinct vectors (points) in Rn into distinct vectors (points) in Rm . That is for each w in the range of T, there is exactly one vector x such that T (x) = w. Theorem 4.10.1: If A is an n × n matrix and TA : Rn → Rn ...
... Definition: A matrix transformation T : Rn → Rm is said to be one-to-one if T maps distinct vectors (points) in Rn into distinct vectors (points) in Rm . That is for each w in the range of T, there is exactly one vector x such that T (x) = w. Theorem 4.10.1: If A is an n × n matrix and TA : Rn → Rn ...
Matrices and Pictures
... There are a large number of pixels at the lower half of the integers, so these values are doubled. The upper half the integers can’t be doubled because the range would be larger than the domain of the colors, so they are set equal to one. Show Slide 9. (Slope) Edge Sharpening: Convolution Convolutio ...
... There are a large number of pixels at the lower half of the integers, so these values are doubled. The upper half the integers can’t be doubled because the range would be larger than the domain of the colors, so they are set equal to one. Show Slide 9. (Slope) Edge Sharpening: Convolution Convolutio ...
Matrices Linear equations Linear Equations
... 2. Find roots (eigenvalues) of the polynomial such that determinant = 0 3. For each eigenvalue solve the equation (1) For larger matrices – alternative ways of computation ...
... 2. Find roots (eigenvalues) of the polynomial such that determinant = 0 3. For each eigenvalue solve the equation (1) For larger matrices – alternative ways of computation ...
Chapter 6: Complex Matrices We assume that the reader has some
... form an orthonormal basis. It turns out that the converse is also true. We have arrived at the following characterization of unitary matrices: An n × n matrix is unitary iff its columns form an orthonormal basis in Cn . Here “iff” stands for “if and only if”, a short hand invented by Paul Halmos. We ...
... form an orthonormal basis. It turns out that the converse is also true. We have arrived at the following characterization of unitary matrices: An n × n matrix is unitary iff its columns form an orthonormal basis in Cn . Here “iff” stands for “if and only if”, a short hand invented by Paul Halmos. We ...
PMV-ALGEBRAS OF MATRICES Department of
... Conversely, if H, W and C are as above then there exists a number µ > 0 such that Γ((Rn , C −1 PH C), µW ) is a product MV-algebra. Throughout we use the notation of (Rn , C −1 PH C) toP indicate the lattice-ordered n real algebra Rn with the positive cone equal precisely i,j=1 R+ C −1 Eij H T C. It ...
... Conversely, if H, W and C are as above then there exists a number µ > 0 such that Γ((Rn , C −1 PH C), µW ) is a product MV-algebra. Throughout we use the notation of (Rn , C −1 PH C) toP indicate the lattice-ordered n real algebra Rn with the positive cone equal precisely i,j=1 R+ C −1 Eij H T C. It ...
Exam2-1010-S13-LinearAlgebra.pdf
... [5] Let V be the vector space of all polynomials of degree 6 3 in the variable x with coefficients in R. Let W be the subspace of polynomials satisfying f(0) = f 0 (0) = 0. Find an orthogonal basis for W with respect to the inner product ...
... [5] Let V be the vector space of all polynomials of degree 6 3 in the variable x with coefficients in R. Let W be the subspace of polynomials satisfying f(0) = f 0 (0) = 0. Find an orthogonal basis for W with respect to the inner product ...
Solving Systems of Equations
... solve for the last variable. Your result will be an ordered triple of the form (x,y,z). Rowechelon form is the goal, although in practice, you don’t always have to let z be the last variable. Graphically, each equation is a plane in three dimensions. We are trying to locate where the three planes in ...
... solve for the last variable. Your result will be an ordered triple of the form (x,y,z). Rowechelon form is the goal, although in practice, you don’t always have to let z be the last variable. Graphically, each equation is a plane in three dimensions. We are trying to locate where the three planes in ...
118 CARL ECKART AND GALE YOUNG each two
... The following definitions will be convenient for the present purpose. An (r, s) matrix is one having r rows and s columns; its elements may be complex numbers. The hermitian transpose of an (r, s) matrix A, whose elements are an, is the (s, r) matrix A* whose elements are (a*)ji = âij. An (V, s) mat ...
... The following definitions will be convenient for the present purpose. An (r, s) matrix is one having r rows and s columns; its elements may be complex numbers. The hermitian transpose of an (r, s) matrix A, whose elements are an, is the (s, r) matrix A* whose elements are (a*)ji = âij. An (V, s) mat ...