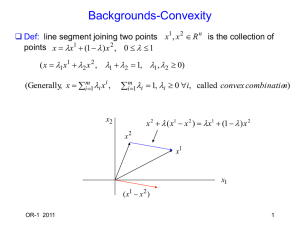
- Free Documents
... .e. there exists a unitary matrix U such that U AU is a triangular matrix. there exists an orthogonal matrix O such that O AO is diagonal. The previous theorem says that there exists a nested sequence of Ainvariant subspaces V V . Theorem Diagonalization For a normal matrix A Cnn . Remark. . i. such ...
... .e. there exists a unitary matrix U such that U AU is a triangular matrix. there exists an orthogonal matrix O such that O AO is diagonal. The previous theorem says that there exists a nested sequence of Ainvariant subspaces V V . Theorem Diagonalization For a normal matrix A Cnn . Remark. . i. such ...
The quadprog Package
... may have arbitrary elements from row mi +1 to row maxmi in the i-th column.) ...
... may have arbitrary elements from row mi +1 to row maxmi in the i-th column.) ...
sequence "``i-lJ-I ioJoilJl``" is in XTexactly when, for every k, the
... for data storage and transmission. The consequences of forbidding a fixed word to occur, which can be considered as a small change or perturbation in the system, are investigated. This situation arises in prefix synchronized codes, where a certain prefix, used to synchronize code words, is forbidden ...
... for data storage and transmission. The consequences of forbidding a fixed word to occur, which can be considered as a small change or perturbation in the system, are investigated. This situation arises in prefix synchronized codes, where a certain prefix, used to synchronize code words, is forbidden ...
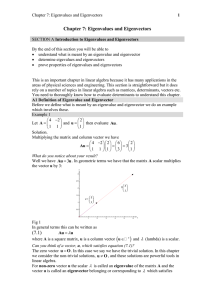
Section 5.1
... The basic concepts presented here - eigenvectors and eigenvalues - are useful throughout pure and applied mathematics. Eigenvalues are also used to study difference equations and continuous dynamical systems. They provide critical information in engineering design, and they arise naturally in such f ...
... The basic concepts presented here - eigenvectors and eigenvalues - are useful throughout pure and applied mathematics. Eigenvalues are also used to study difference equations and continuous dynamical systems. They provide critical information in engineering design, and they arise naturally in such f ...
Lecture 2: Spectra of Graphs 1 Definitions
... 3. If G is connected, then G is bipartite iff λn = −d. Lemma 2.7. All eigenvalues of L are non-negative. Proof. Follows from Lemma 2.6 and the definition of L = D − A. For studying regular graphs, it is convenient to work with the normalized adjacency matrix M of graph G. For any d-regular graph wit ...
... 3. If G is connected, then G is bipartite iff λn = −d. Lemma 2.7. All eigenvalues of L are non-negative. Proof. Follows from Lemma 2.6 and the definition of L = D − A. For studying regular graphs, it is convenient to work with the normalized adjacency matrix M of graph G. For any d-regular graph wit ...
topological invariants of knots and links
... Moreover, these last two curves may be regarded as the diagram curves of a pair of non-interlinking knots Ki and K2 in space. If neither of the knots Ki nor K2 is unknotted we may regard Ki and K2 as factors of the composite knot K. If one of them, Ku is unknotted, the knot K must evidently be of th ...
... Moreover, these last two curves may be regarded as the diagram curves of a pair of non-interlinking knots Ki and K2 in space. If neither of the knots Ki nor K2 is unknotted we may regard Ki and K2 as factors of the composite knot K. If one of them, Ku is unknotted, the knot K must evidently be of th ...
On the Kemeny constant and stationary distribution vector
... distribution vector when A is perturbed, with small values of the Kemeny constant corresponding to well–conditioned stationary distribution vectors. In view of these last observations regarding low values of the Kemeny constant, it is not surprising that there is interest in identifying stochastic m ...
... distribution vector when A is perturbed, with small values of the Kemeny constant corresponding to well–conditioned stationary distribution vectors. In view of these last observations regarding low values of the Kemeny constant, it is not surprising that there is interest in identifying stochastic m ...
S.M. Rump. On P-Matrices. Linear Algebra and its Applications
... The table shows that for these parametrized test sets the gap between the necessary condition and the sufficient condition given in Theorem 3.4 is not too large. This statement need not to extend to other test sets, as will be seen in the next section. 4. A not a priori exponential check of P -prope ...
... The table shows that for these parametrized test sets the gap between the necessary condition and the sufficient condition given in Theorem 3.4 is not too large. This statement need not to extend to other test sets, as will be seen in the next section. 4. A not a priori exponential check of P -prope ...