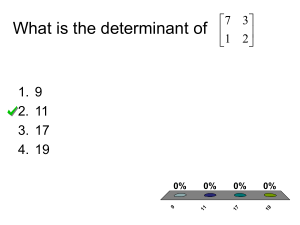
PMV-ALGEBRAS OF MATRICES Department of
... indicate the lattice-ordered n real algebra Rn with the positive cone equal precisely i,j=1 R+ C −1 Eij H T C. It is proven in Ma and Wojciechowski [4] that any lattice-ordered algebra Rn is of this form. Particular structure of the basic elements of those orders are discussed there. We need the fol ...
... indicate the lattice-ordered n real algebra Rn with the positive cone equal precisely i,j=1 R+ C −1 Eij H T C. It is proven in Ma and Wojciechowski [4] that any lattice-ordered algebra Rn is of this form. Particular structure of the basic elements of those orders are discussed there. We need the fol ...
Matrices Linear equations Linear Equations
... If there are no zero eigenvalues – matrix is invertible If there are no repeated eigenvalues – matrix is diagonalizable If all the eigenvalues are different then eigenvectors are linearly independent ...
... If there are no zero eigenvalues – matrix is invertible If there are no repeated eigenvalues – matrix is diagonalizable If all the eigenvalues are different then eigenvectors are linearly independent ...
MTH 264 SECTION 3.3 20 DELTA COLLEGE The slope field for the
... The characteristic equation of this matrix is: λ2 − 16 = 0. This equation factors into (λ − 4)(λ + 4) = 0, and so it has two distinct, real roots: λ1 = 4 and λ2 = −4. Since one eigenvalue is positive and one eigenvalue is negative, the equilibrium point at the origin is a saddle. (b) For eigenvalue ...
... The characteristic equation of this matrix is: λ2 − 16 = 0. This equation factors into (λ − 4)(λ + 4) = 0, and so it has two distinct, real roots: λ1 = 4 and λ2 = −4. Since one eigenvalue is positive and one eigenvalue is negative, the equilibrium point at the origin is a saddle. (b) For eigenvalue ...
Matrix operations
... A, B, and C are all matrices. It is assumed that A, B and C all have the same size, so that addition can be performed. • A + B = B + A (commutative property of addition) • A + (B + C) = (A + B) + C (associative property of addition) • A + 0 = 0 + A = A (additive identity property. The 0 is a 0 matri ...
... A, B, and C are all matrices. It is assumed that A, B and C all have the same size, so that addition can be performed. • A + B = B + A (commutative property of addition) • A + (B + C) = (A + B) + C (associative property of addition) • A + 0 = 0 + A = A (additive identity property. The 0 is a 0 matri ...