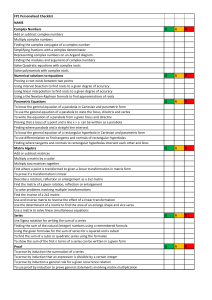
Exercise 4
... transformation matrix S has been found, the eigenvectors of A are contained in the columns of the transformation matrix on the right in Eq. 7 and in the rows of its inverse in Eq. 7, S-1. The eigenvalues A are the diagonal elements of A' and the eigenvalue in the nth diagonal element corresponds to ...
... transformation matrix S has been found, the eigenvectors of A are contained in the columns of the transformation matrix on the right in Eq. 7 and in the rows of its inverse in Eq. 7, S-1. The eigenvalues A are the diagonal elements of A' and the eigenvalue in the nth diagonal element corresponds to ...
Multiplication of Matrices
... and x = C●,k is a column vector. On the other hand by the first definition of matrix multiplication ((AB)C)ik = ((AB)i,●)(C●,k). By the third definition of matrix multiplication (AB)i,● = (Ai,●)B. So ((AB)C)ik = ((Ai,●)B)(C●,k) = (pB)x. However, in the previous section we proved that if p is a row v ...
... and x = C●,k is a column vector. On the other hand by the first definition of matrix multiplication ((AB)C)ik = ((AB)i,●)(C●,k). By the third definition of matrix multiplication (AB)i,● = (Ai,●)B. So ((AB)C)ik = ((Ai,●)B)(C●,k) = (pB)x. However, in the previous section we proved that if p is a row v ...
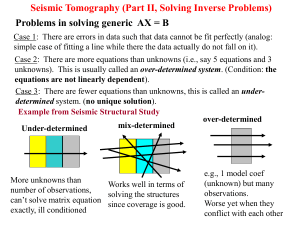
![[1] Eigenvectors and Eigenvalues](http://s1.studyres.com/store/data/014314239_1-836177f5554eb265785889c7c5fb970f-300x300.png)
[1] Eigenvectors and Eigenvalues
... initial conditions y1 (0) and y2 (0). It makes sense to multiply by this parameter because when we have an eigenvector, we actually have an entire line of eigenvectors. And this line of eigenvectors gives us a line of solutions. This is what we’re looking for. Note that this is the general solution ...
... initial conditions y1 (0) and y2 (0). It makes sense to multiply by this parameter because when we have an eigenvector, we actually have an entire line of eigenvectors. And this line of eigenvectors gives us a line of solutions. This is what we’re looking for. Note that this is the general solution ...
