Algebra 3 – Chapter 10 – Matrices
... To add/subtract matrices, we add/subtract the corresponding elements. The matrices must have the same dimensions. Capital letters are used to denote matrices. A matrix having zeros for all of its members or elements is called a zero matrix and is often denoted as O. When a zero matrix is added to an ...
... To add/subtract matrices, we add/subtract the corresponding elements. The matrices must have the same dimensions. Capital letters are used to denote matrices. A matrix having zeros for all of its members or elements is called a zero matrix and is often denoted as O. When a zero matrix is added to an ...
Case Study: Space Flight and Control Systems
... The crossed circles are called summing junctions; signals are combined at these points for delivery to some process as input. For example, the commanded pitch is summed with input from the inertial measuring unit, which produces a pitch rate that is used by process K1 as input. Notice that this syst ...
... The crossed circles are called summing junctions; signals are combined at these points for delivery to some process as input. For example, the commanded pitch is summed with input from the inertial measuring unit, which produces a pitch rate that is used by process K1 as input. Notice that this syst ...
![[Review published in SIAM Review, Vol. 56, Issue 1, pp. 189–191.]](http://s1.studyres.com/store/data/017041202_1-65d6c90f40ee4c0571100dd75b61a7f5-300x300.png)
In algebra, a determinant is a function depending on
... understanding, the sign of the determinant of a basis can be used to define the notion of orientation in Euclidean spaces. The determinant of a set of vectors is positive if the vectors form a right-handed coordinate system, and negative if left-handed. Determinants are used to calculate volumes in ...
... understanding, the sign of the determinant of a basis can be used to define the notion of orientation in Euclidean spaces. The determinant of a set of vectors is positive if the vectors form a right-handed coordinate system, and negative if left-handed. Determinants are used to calculate volumes in ...
immanants of totally positive matrices are nonnegative
... If/ is an irreducible character of Sn, these functions are known as immanants; if/ is an irreducible character of some subgroup G of Sn (extended trivially to all of Sn by defining /(vv) = 0 for w$G), these are known as generalized matrix functions. Note that the determinant and permanent are obtain ...
... If/ is an irreducible character of Sn, these functions are known as immanants; if/ is an irreducible character of some subgroup G of Sn (extended trivially to all of Sn by defining /(vv) = 0 for w$G), these are known as generalized matrix functions. Note that the determinant and permanent are obtain ...
**** 1 - DCASL
... This characteristic Eq. is the same as the desired characteristic Eq. for the system, when ‘u = -Kx’ is used as the control signal. ...
... This characteristic Eq. is the same as the desired characteristic Eq. for the system, when ‘u = -Kx’ is used as the control signal. ...
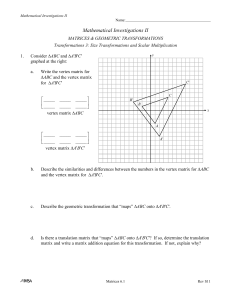
6.4 Dilations
... You should have noticed that in mapping ABC onto A'B'C', all of coordinates were doubled in the first problem and all of the coordinates were halved in the second problem. In addition, it should have been clear that there is no translation matrix that maps ABC onto A'B'C' because the two triangl ...
... You should have noticed that in mapping ABC onto A'B'C', all of coordinates were doubled in the first problem and all of the coordinates were halved in the second problem. In addition, it should have been clear that there is no translation matrix that maps ABC onto A'B'C' because the two triangl ...
1 Gaussian elimination: LU
... i.e., Gaussian elimination gives us the LU -factorization (sometimes also called the LU -decomposition) of the matrix A, A = LU , where L is a lower triangular matrix with all diagonal entries equal to 1, and U is an upper triangular matrix. Once we have this factorization, how can we make use of i ...
... i.e., Gaussian elimination gives us the LU -factorization (sometimes also called the LU -decomposition) of the matrix A, A = LU , where L is a lower triangular matrix with all diagonal entries equal to 1, and U is an upper triangular matrix. Once we have this factorization, how can we make use of i ...
Cards HS Number and Quantity
... geometrically on the complex plane; use properties of this representation for computation. For example, (-1 + √3 i)3 = 8 because (-1 + √3 i) has modulus 2 and argument 120°. ...
... geometrically on the complex plane; use properties of this representation for computation. For example, (-1 + √3 i)3 = 8 because (-1 + √3 i) has modulus 2 and argument 120°. ...
Non-negative matrix factorization
NMF redirects here. For the bridge convention, see new minor forcing.Non-negative matrix factorization (NMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix V is factorized into (usually) two matrices W and H, with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically.NMF finds applications in such fields as computer vision, document clustering, chemometrics, audio signal processing and recommender systems.