x that passes through the point (2, 4)
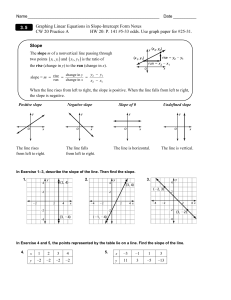
... first line, y = - 1x ? This is in slope intercept form so y = mx + b which means the slope is –1. ...
... first line, y = - 1x ? This is in slope intercept form so y = mx + b which means the slope is –1. ...
Novel simulation methods for Coulomb and hydrodynamic interactions
... a system of slow Brownian particles (in our case: monomers which are connected to build polymer chains), immersed in a viscous fluid. The fast momentum transport through the solvent induces long-range correlations in the stochastic displacements. It is possible to explicitly simulate the solvent deg ...
... a system of slow Brownian particles (in our case: monomers which are connected to build polymer chains), immersed in a viscous fluid. The fast momentum transport through the solvent induces long-range correlations in the stochastic displacements. It is possible to explicitly simulate the solvent deg ...
MATH 212
... each chapter of the text. Assignment must be presented either in an 8 21 11 “blue book” or submitted to me by E-mail as a .pdf …le. 3) The only attendance requirement is that you complete the MDTP CR test within the …rst two weeks of class: Go to mdtp.ucsd.edu, click on On-Line Tests and select the ...
... each chapter of the text. Assignment must be presented either in an 8 21 11 “blue book” or submitted to me by E-mail as a .pdf …le. 3) The only attendance requirement is that you complete the MDTP CR test within the …rst two weeks of class: Go to mdtp.ucsd.edu, click on On-Line Tests and select the ...
A new code for the Hall-driven magnetic evolution of neutron...
... components of ∇ along the edges of the cell. Stokes’ theorem allows us to write the curl components in terms of the MF components defined at the cell faces. As an example, we show in Fig. 1 the location of the variables in a numerical cell in spherical coordinates (r, θ, ϕ) and assuming axial symmet ...
... components of ∇ along the edges of the cell. Stokes’ theorem allows us to write the curl components in terms of the MF components defined at the cell faces. As an example, we show in Fig. 1 the location of the variables in a numerical cell in spherical coordinates (r, θ, ϕ) and assuming axial symmet ...
Partial differential equation

In mathematics, a partial differential equation (PDE) is a differential equation that contains unknown multivariable functions and their partial derivatives. (A special case are ordinary differential equations (ODEs), which deal with functions of a single variable and their derivatives.) PDEs are used to formulate problems involving functions of several variables, and are either solved by hand, or used to create a relevant computer model.PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid flow, elasticity, or quantum mechanics. These seemingly distinct physical phenomena can be formalised similarly in terms of PDEs. Just as ordinary differential equations often model one-dimensional dynamical systems, partial differential equations often model multidimensional systems. PDEs find their generalisation in stochastic partial differential equations.