Classical Mechanics - Mathematical Institute Course Management
... of Nature. Scientists, even theoretical physicists, will often try to revert to using the techniques of classical mechanics where possible. Indeed, measuring the differences from Newtonian theory usually requires very well-designed and delicate experiments. From a computational point of view Newton ...
... of Nature. Scientists, even theoretical physicists, will often try to revert to using the techniques of classical mechanics where possible. Indeed, measuring the differences from Newtonian theory usually requires very well-designed and delicate experiments. From a computational point of view Newton ...
BOLTZMANN`S ENTROPY AND TIME`S ARROW
... universe, measurement is a new source of irreversibility; rather, I believe that real measurements on quantum systems are time asymmetric because they involve, of necessity, systems, such as measuring apparatus, with a very large number of degrees of freedom. Quantum irreversibility should and can b ...
... universe, measurement is a new source of irreversibility; rather, I believe that real measurements on quantum systems are time asymmetric because they involve, of necessity, systems, such as measuring apparatus, with a very large number of degrees of freedom. Quantum irreversibility should and can b ...
Level Set and Phase Field Methods: Application to
... solutions. One possibility is the "swallowtail" solution, which is formed by letting the front pass through itself. However, if the moving curve is regarded as a physical interface separating two regions, this solution wouldn't be meaningful. A more physically reasonable weak solution can be obtaine ...
... solutions. One possibility is the "swallowtail" solution, which is formed by letting the front pass through itself. However, if the moving curve is regarded as a physical interface separating two regions, this solution wouldn't be meaningful. A more physically reasonable weak solution can be obtaine ...
One-Class Support Measure Machines for Group Anomaly Detection
... The anomaly detection has been intensively studied (Chandola et al. (2009) and references therein). However, few attempts have been made on developing successful group anomaly detection algorithms. For example, a straightforward approach is to define a set of features for each group and apply standa ...
... The anomaly detection has been intensively studied (Chandola et al. (2009) and references therein). However, few attempts have been made on developing successful group anomaly detection algorithms. For example, a straightforward approach is to define a set of features for each group and apply standa ...
here.
... reproduces Newton’s equation. We denote coordinates by q rather than x to emphasize they need not be Cartesian coordinates. Let us briefly describe how Lagrange’s equations arise. • We consider the problem of determining the classical trajectory that a particle must take if it was at qi at ti and q ...
... reproduces Newton’s equation. We denote coordinates by q rather than x to emphasize they need not be Cartesian coordinates. Let us briefly describe how Lagrange’s equations arise. • We consider the problem of determining the classical trajectory that a particle must take if it was at qi at ti and q ...
JQE vol28, pp. 2631 - d
... the fundamental and second-harmonic waves travel at different phase velocities. Since the sign of power flow from one wave to the other is determined by the relative phase between the waves, the continuous phase slip between these waves caused by their differing phase velocities leads to an alternat ...
... the fundamental and second-harmonic waves travel at different phase velocities. Since the sign of power flow from one wave to the other is determined by the relative phase between the waves, the continuous phase slip between these waves caused by their differing phase velocities leads to an alternat ...
Lecture Notes for College Physics I
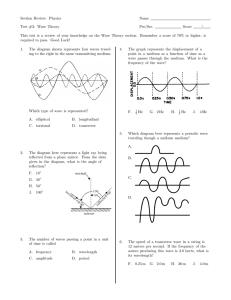
... Kinematics is the part of Physics that contains the terminology used to describe the motion of particles. For this purpose, the first element of the kinematic description of the motion of a particle involves tracking its position as a function of time. Because the motion of the particle may involve ...
... Kinematics is the part of Physics that contains the terminology used to describe the motion of particles. For this purpose, the first element of the kinematic description of the motion of a particle involves tracking its position as a function of time. Because the motion of the particle may involve ...
Spin density waves in bilayer cold polar molecules
... extremely short-range and is labeled as the so-called contact interaction. Indeed, ultracold molecules offer a diverse scientific direction and promised application such as study of novel dynamics in the low-energy collisions, long-range collective quantum effects and quantum phase transitions, prec ...
... extremely short-range and is labeled as the so-called contact interaction. Indeed, ultracold molecules offer a diverse scientific direction and promised application such as study of novel dynamics in the low-energy collisions, long-range collective quantum effects and quantum phase transitions, prec ...
Wave packet
.gif?width=300)
In physics, a wave packet (or wave train) is a short ""burst"" or ""envelope"" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant (no dispersion, see figure) or it may change (dispersion) while propagating.Quantum mechanics ascribes a special significance to the wave packet; it is interpreted as a probability amplitude, its norm squared describing the probability density that a particle or particles in a particular state will be measured to have a given position or momentum. The wave equation is in this case the Schrödinger equation. It is possible to deduce the time evolution of a quantum mechanical system, similar to the process of the Hamiltonian formalism in classical mechanics. The dispersive character of solutions of the Schrödinger equation has played an important role in rejecting Schrödinger's original interpretation, and accepting the Born rule.In the coordinate representation of the wave (such as the Cartesian coordinate system), the position of the physical object's localized probability is specified by the position of the packet solution. Moreover, the narrower the spatial wave packet, and therefore the better localized the position of the wave packet, the larger the spread in the momentum of the wave. This trade-off between spread in position and spread in momentum is a characteristic feature of the Heisenberg uncertainty principle,and will be illustrated below.