Central Tendency and Variability
... • Definition: descriptive stat that best represents the center of a distribution of data. • Mean: arithmetic average – “Typical score” – Often described as the “middle” of the scores, so don’t confuse this with medians. ...
... • Definition: descriptive stat that best represents the center of a distribution of data. • Mean: arithmetic average – “Typical score” – Often described as the “middle” of the scores, so don’t confuse this with medians. ...
1. JLD Engineering is supplied a part from two different companies
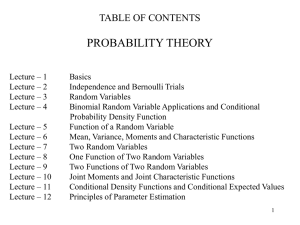
... Statistics Revision Pack 4 - Probabiilty ...
... Statistics Revision Pack 4 - Probabiilty ...
Paradoxes in Probability Theory
... from 1933 [Ko], the focus being on calculating or estimating probabilities or expectations of various events or quantities in such models. In contrast, issues about how to choose a probability model suitable for a particular real-world situation (or for a particular philosophical thought experiment) ...
... from 1933 [Ko], the focus being on calculating or estimating probabilities or expectations of various events or quantities in such models. In contrast, issues about how to choose a probability model suitable for a particular real-world situation (or for a particular philosophical thought experiment) ...
Lecture 9: Bayesian hypothesis testing
... Before we go into the details of Bayesian hypothesis testing, let us briefly review frequentist hypothesis testing. Recall that in the Neyman-Pearson paradigm characteristic of frequentist hypothesis testing, there is an asymmetric relationship between two hypotheses: the null hypothesis H0 and the ...
... Before we go into the details of Bayesian hypothesis testing, let us briefly review frequentist hypothesis testing. Recall that in the Neyman-Pearson paradigm characteristic of frequentist hypothesis testing, there is an asymmetric relationship between two hypotheses: the null hypothesis H0 and the ...
Paradoxes in Probability Theory, by William
... Of these seven paradoxes, two are new, whereas the other five are known from the literature – such as the Simulation Argument, which was put forth by Bostrom [B] in 2003 and has been the topic of intense discussion in the philosophy literature ever since.4 The two new ones – the Betting Crowd and th ...
... Of these seven paradoxes, two are new, whereas the other five are known from the literature – such as the Simulation Argument, which was put forth by Bostrom [B] in 2003 and has been the topic of intense discussion in the philosophy literature ever since.4 The two new ones – the Betting Crowd and th ...
Problem 1 - Art of Problem Solving
... - Up to three heads follow, but then tails. In order to have a chance at success, the flip after tails must be heads. If it is, then a new run begins with heads, which is neutral. (That means success is independent of these flips.) ...
... - Up to three heads follow, but then tails. In order to have a chance at success, the flip after tails must be heads. If it is, then a new run begins with heads, which is neutral. (That means success is independent of these flips.) ...
Learning and designing stochastic processes from logical constraints
... Conceptually, both model checking and statistical model checking start from the premise that a CTMC model of the system is entirely specified, i.e. the underlying parameters of the CTMC are known exactly. This is generally not true: it is certainly never true when employing CTMCs as models of physic ...
... Conceptually, both model checking and statistical model checking start from the premise that a CTMC model of the system is entirely specified, i.e. the underlying parameters of the CTMC are known exactly. This is generally not true: it is certainly never true when employing CTMCs as models of physic ...
Statistics and probability: Chance
... E′ M E b FE c (M E) F d e If a positive integer less than 12 is selected at random, what is the probability that it is not a factor of 12, an even number or a multiple of 10? ...
... E′ M E b FE c (M E) F d e If a positive integer less than 12 is selected at random, what is the probability that it is not a factor of 12, an even number or a multiple of 10? ...
Creating Probability Models for Simple Events
... looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cas ...
... looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cas ...
Probability box
),steps=500.png?width=300)
A probability box (or p-box) is a characterization of an uncertain number consisting of both aleatoric and epistemic uncertainties that is often used in risk analysis or quantitative uncertainty modeling where numerical calculations must be performed. Probability bounds analysis is used to make arithmetic and logical calculations with p-boxes.An example p-box is shown in the figure at right for an uncertain number x consisting of a left (upper) bound and a right (lower) bound on the probability distribution for x. The bounds are coincident for values of x below 0 and above 24. The bounds may have almost any shapes, including step functions, so long as they are monotonically increasing and do not cross each other. A p-box is used to express simultaneously incertitude (epistemic uncertainty), which is represented by the breadth between the left and right edges of the p-box, and variability (aleatory uncertainty), which is represented by the overall slant of the p-box.