Quadratic Equations - Recruitments Today
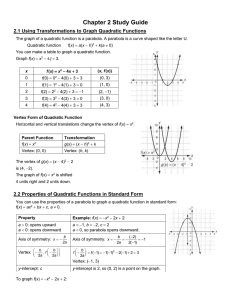
... This one is a little more tricky: Where is a? In fact a=1, as we don't usually write "1x2“ b = -3 and where is c? Well, c=0, so is not shown. ...
... This one is a little more tricky: Where is a? In fact a=1, as we don't usually write "1x2“ b = -3 and where is c? Well, c=0, so is not shown. ...
Solutions
... inequality here holds whether or not the extensions are separable. You should try to prove it in this generality.) Certainly, [EF : K] = [EF : F ][F : K]. Hence, it suffices to show that [EF : F ] ≤ [E : K]. Let β1 , . . . , βn be a K-basis for F . So F = Kβ1 + · · · + Kβn . Then using the second st ...
... inequality here holds whether or not the extensions are separable. You should try to prove it in this generality.) Certainly, [EF : K] = [EF : F ][F : K]. Hence, it suffices to show that [EF : F ] ≤ [E : K]. Let β1 , . . . , βn be a K-basis for F . So F = Kβ1 + · · · + Kβn . Then using the second st ...
Computer-Generated Proofs of Mathematical Theorems
... Mathematics is frequently viewed as a formal language with clearly established underlying assumptions or axioms and unambiguous rules for determining the truth of every statement couched in this language. In the early decades of the twentieth century, works such as Russell and Whitehead’s Principia ...
... Mathematics is frequently viewed as a formal language with clearly established underlying assumptions or axioms and unambiguous rules for determining the truth of every statement couched in this language. In the early decades of the twentieth century, works such as Russell and Whitehead’s Principia ...
Variations on Belyi`s theorem - Universidad Autónoma de Madrid
... easy to apply (at least by us, the non experts) since, as often occurs in practice, it is difficult to check if its hypotheses are satisfied in a given problem (cf. [27]). On the contrary, our criterion (Criterion 1) is easy to handle. Although it is much less ambitious, in that it only attempts to det ...
... easy to apply (at least by us, the non experts) since, as often occurs in practice, it is difficult to check if its hypotheses are satisfied in a given problem (cf. [27]). On the contrary, our criterion (Criterion 1) is easy to handle. Although it is much less ambitious, in that it only attempts to det ...
Solving With Or Without Equations
... is at infinity and a simple geometric construction shows that there are always pentahedra with parallel edges AD, BE, CF , except when some triangular or tetrahedric inequality is violated. Finally, there are 6 spurious roots, where the pentahedron is flat, so edges AD, BE, CF need not be concurrent ...
... is at infinity and a simple geometric construction shows that there are always pentahedra with parallel edges AD, BE, CF , except when some triangular or tetrahedric inequality is violated. Finally, there are 6 spurious roots, where the pentahedron is flat, so edges AD, BE, CF need not be concurrent ...
Hovhannes Khudaverdian's notes
... To prove that r.h.s. of the formula above is equal to 3 you have to use the fact that equation x3 − 3x − 18 has the solution x = 3. Vicious circle???! Another problem with formula (2): Consider the polynomial: x3 − 7x + 6 = (x − 1)(x − 2)(x + 3) ...
... To prove that r.h.s. of the formula above is equal to 3 you have to use the fact that equation x3 − 3x − 18 has the solution x = 3. Vicious circle???! Another problem with formula (2): Consider the polynomial: x3 − 7x + 6 = (x − 1)(x − 2)(x + 3) ...
x + 1 - mrhubbard
... Example 3: 15x - 3xy + 4y - 20 (15x - 3xy) + (4y - 20) Group 3x(5 - y) + 4(y - 5) Factor GCF 3x(-1)(-5 + y) + 4(y - 5) Notice additive inverses -3x(y - 5) + 4(y - 5) Simplify (y - 5) (-3x + 4) Factor common binomial Remember to check each problem by using FOIL. ...
... Example 3: 15x - 3xy + 4y - 20 (15x - 3xy) + (4y - 20) Group 3x(5 - y) + 4(y - 5) Factor GCF 3x(-1)(-5 + y) + 4(y - 5) Notice additive inverses -3x(y - 5) + 4(y - 5) Simplify (y - 5) (-3x + 4) Factor common binomial Remember to check each problem by using FOIL. ...
Homology With Local Coefficients
... We shalldeal onlywithpropertiesofsystemswhichare invariantunderisomorphisms. In each case theproofofinvarianceis trivialand willbe omitted. It was proved in ?2 that the collection {Fx} is a systemof local groups. It is simpleif and only if it is abelian. In some instances a system {G1, will consist ...
... We shalldeal onlywithpropertiesofsystemswhichare invariantunderisomorphisms. In each case theproofofinvarianceis trivialand willbe omitted. It was proved in ?2 that the collection {Fx} is a systemof local groups. It is simpleif and only if it is abelian. In some instances a system {G1, will consist ...